Surgery obstruction
In mathematics, specifically in surgery theory, the surgery obstructions define a map 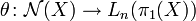 from the normal invariants to the L-groups which is in the first instance a set-theoretic map (that means not necessarily a homomorphism) with the following property when
from the normal invariants to the L-groups which is in the first instance a set-theoretic map (that means not necessarily a homomorphism) with the following property when 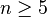 :
:
A degree-one normal map 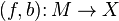 is normally cobordant to a homotopy equivalence if and only if the image
is normally cobordant to a homotopy equivalence if and only if the image 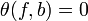 in
in ![L_n (\mathbb{Z} [\pi_1 (X)])](../I/m/19d12e180ac30aed6f70050eefc259e7.png) .
.
Sketch of the definition
The surgery obstruction of a degree-one normal map has a relatively complicated definition.
Consider a degree-one normal map 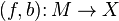 . The idea in deciding the question whether it is normally cobordant to a homotopy equivalence is to try to systematically improve
. The idea in deciding the question whether it is normally cobordant to a homotopy equivalence is to try to systematically improve 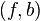 so that the map
so that the map  becomes
becomes  -connected (that means the homotopy groups
-connected (that means the homotopy groups 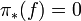 for
for 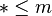 ) for high
) for high  . It is a consequence of Poincaré duality that if we can achieve this for
. It is a consequence of Poincaré duality that if we can achieve this for 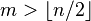 then the map
then the map  already is a homotopy equivalence. The word systematically above refers to the fact that one tries to do surgeries on
already is a homotopy equivalence. The word systematically above refers to the fact that one tries to do surgeries on  to kill elements of
to kill elements of 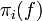 . In fact it is more convenient to use homology of the universal covers to observe how connected the map
. In fact it is more convenient to use homology of the universal covers to observe how connected the map  is. More precisely, one works with the surgery kernels
is. More precisely, one works with the surgery kernels 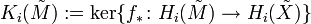 which one views as
which one views as ![\mathbb{Z}[\pi_1 (X)]](../I/m/5190bf58db63858b172b22788eafb6bd.png) -modules. If all these vanish, then the map
-modules. If all these vanish, then the map  is a homotopy equivalence. As a consequence of Poincaré duality on
is a homotopy equivalence. As a consequence of Poincaré duality on  and
and  there is a
there is a ![\mathbb{Z}[\pi_1 (X)]](../I/m/5190bf58db63858b172b22788eafb6bd.png) -modules Poincaré duality
-modules Poincaré duality 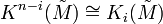 , so one only has to watch half of them, that means those for which
, so one only has to watch half of them, that means those for which 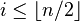 .
.
Any degree-one normal map can be made 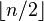 -connected by the process called surgery below the middle dimension. This is the process of killing elements of
-connected by the process called surgery below the middle dimension. This is the process of killing elements of 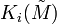 for
for 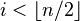 described here when we have
described here when we have 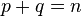 such that
such that 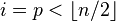 . After this is done there are two cases.
. After this is done there are two cases.
1. If 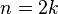 then the only nontrivial homology group is the kernel
then the only nontrivial homology group is the kernel 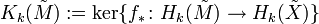 . It turns out that the cup-product pairings on
. It turns out that the cup-product pairings on  and
and  induce a cup-product pairing on
induce a cup-product pairing on 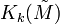 . This defines a symmetric bilinear form in case
. This defines a symmetric bilinear form in case 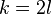 and a skew-symmetric bilinear form in case
and a skew-symmetric bilinear form in case 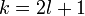 . It turns out that these forms can be refined to
. It turns out that these forms can be refined to  -quadratic forms, where
-quadratic forms, where 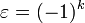 . These
. These  -quadratic forms define elements in the L-groups
-quadratic forms define elements in the L-groups 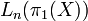 .
.
2. If 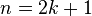 the definition is more complicated. Instead of a quadratic form one obtains from the geometry a quadratic formation, which is a kind of automorphism of quadratic forms. Such a thing defines an element in the odd-dimensional L-group
the definition is more complicated. Instead of a quadratic form one obtains from the geometry a quadratic formation, which is a kind of automorphism of quadratic forms. Such a thing defines an element in the odd-dimensional L-group 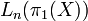 .
.
If the element 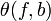 is zero in the L-group surgery can be done on
is zero in the L-group surgery can be done on  to modify
to modify  to a homotopy equivalence.
to a homotopy equivalence.
Geometrically the reason why this is not always possible is that performing surgery in the middle dimension to kill an element in 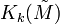 possibly creates an element in
possibly creates an element in 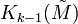 when
when 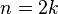 or in
or in 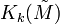 when
when 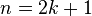 . So this possibly destroys what has already been achieved. However, if
. So this possibly destroys what has already been achieved. However, if 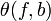 is zero, surgeries can be arranged in such a way that this does not happen.
is zero, surgeries can be arranged in such a way that this does not happen.
Example
In the simply connected case the following happens.
If 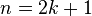 there is no obstruction.
there is no obstruction.
If 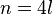 then the surgery obstruction can be calculated as the difference of the signatures of M and X.
then the surgery obstruction can be calculated as the difference of the signatures of M and X.
If 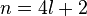 then the surgery obstruction is the Arf-invariant of the associated kernel quadratic form over
then the surgery obstruction is the Arf-invariant of the associated kernel quadratic form over 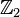 .
.
References
- Browder, William (1972), Surgery on simply-connected manifolds, Berlin, New York: Springer-Verlag, MR 0358813
- Lück, Wolfgang (2002), A basic introduction to surgery theory, ICTP Lecture Notes Series 9, Band 1, of the school "High-dimensional manifold theory" in Trieste, May/June 2001, Abdus Salam International Centre for Theoretical Physics, Trieste 1-224
- Ranicki, Andrew (2002), Algebraic and Geometric Surgery, Oxford Mathematical Monographs, Clarendon Press, ISBN 978-0-19-850924-0, MR 2061749
- Wall, C. T. C. (1999), Surgery on compact manifolds, Mathematical Surveys and Monographs 69 (2nd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0942-6, MR 1687388