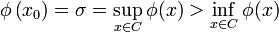Supporting functional

In convex analysis and mathematical optimization, the supporting functional is a generalization of the supporting hyperplane of a set.

Mathematical definition

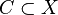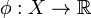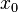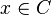Let X be a locally convex topological space, and $C \subset X$ be a convex set, then the continuous linear functional $\phi: X \to \mathbb{R}$ is a supporting functional of C at the point $x_0$ if $\phi(x) \leq \phi(x_0)$ for every $x \in C$ .^[1]

Relation to support function

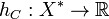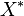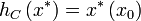If $h_C: X^* \to \mathbb{R}$ (where $X^*$ is the dual space of $X$ ) is a support function of the set C, then if $h_C\left(x^*\right) = x^*\left(x_0\right)$ , it follows that 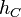$h_C$ defines a supporting functional 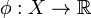$\phi: X \to \mathbb{R}$ of C at the point 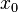$x_0$ such that 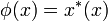$\phi(x) = x^*(x)$ for any $x \in X$ .

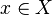Relation to supporting hyperplane

If $\phi$ is a supporting functional of the convex set C at the point $x_0 \in C$ such that

\phi\left(x_0\right) = \sigma = \sup_{x \in C} \phi(x) > \inf_{x \in C} \phi(x)

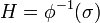then $H = \phi^{-1}(\sigma)$ defines a supporting hyperplane to C at 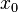$x_0$ .^[2]

References

↑ Pallaschke, Diethard; Rolewicz, Stefan (1997). Foundations of mathematical optimization: convex analysis without linearity. Springer. p. 323. ISBN 978-0-7923-4424-7.
↑ Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. p. 240. ISBN 978-0-387-29570-1.