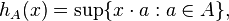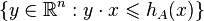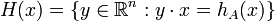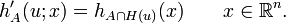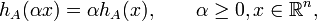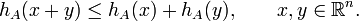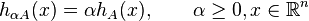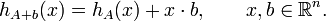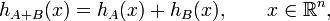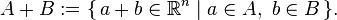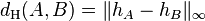Support function
In mathematics, the support function hA of a non-empty closed convex set A in 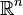 describes the (signed) distances of supporting hyperplanes of A from the origin. The support function is a convex function on
describes the (signed) distances of supporting hyperplanes of A from the origin. The support function is a convex function on 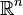 .
Any non-empty closed convex set A is uniquely determined by hA. Furthermore the support function, as a function of the set A is compatible with many natural geometric operations, like scaling, translation, rotation and Minkowski addition.
Due to these properties, the support function is one of the most central basic concepts in convex geometry.
.
Any non-empty closed convex set A is uniquely determined by hA. Furthermore the support function, as a function of the set A is compatible with many natural geometric operations, like scaling, translation, rotation and Minkowski addition.
Due to these properties, the support function is one of the most central basic concepts in convex geometry.
Definition
The support function 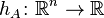 of a non-empty closed convex set A in
of a non-empty closed convex set A in 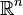 is given by
is given by
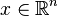 ; see
[1]
[2]
.[3] Its interpretation is most intuitive when x is a unit vector:
by definition, A is contained in the closed half space
; see
[1]
[2]
.[3] Its interpretation is most intuitive when x is a unit vector:
by definition, A is contained in the closed half space
and there is at least one point of A in the boundary
of this half space. The hyperplane H(x) is therefore called a supporting hyperplane with exterior (or outer) unit normal vector x. The word exterior is important here, as the orientation of x plays a role, the set H(x) is in general different from H(-x). Now hA is the (signed) distance of H(x) from the origin.
Examples
The support function of a singleton A={a} is  .
.
The support function of the Euclidean unit ball B1 is 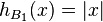 .
.
If A is a line segment through the origin with endpoints -a and a then 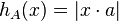 .
.
Properties
As a function of x
The support function of a compact convex set is real valued and continuous, but if the
set is unbounded, its support function is extended real valued (it takes the value
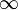 ). As any nonempty closed convex set is the intersection of
its supporting half spaces, the function hA determines A uniquely.
This can be used to describe certain geometric properties of convex sets analytically.
For instance, a set A is point symmetric with respect to the origin if and only hA
is an even function.
). As any nonempty closed convex set is the intersection of
its supporting half spaces, the function hA determines A uniquely.
This can be used to describe certain geometric properties of convex sets analytically.
For instance, a set A is point symmetric with respect to the origin if and only hA
is an even function.
In general, the support function is not differentiable. However, directional derivatives exist and yield support functions of support sets. If A is compact and convex, and hA'(u;x) denotes the directional derivative of hA at u ≠ 0 in direction x, we have
Here H(u) is the supporting hyperplane of A with exterior normal vector u, defined above. If A ∩ H(u) is a sinlgeton {y}, say, it follows that the support function is differentable at u and its gradient coincides with y. Conversely, if hA is differentiable at u, then A ∩ H(u) is a sinlgeton. Hence hA is differentable at all points u ≠ 0 if and only if A is strictly convex (the boundary of A does not contain any line segments).
It follows directly from its definition that the support function is positive homogeneous:
and subadditive:
It follows that hA is a convex function.
It is crucial in convex geometry that these properties characterize support functions:
Any positive homogeneous, convex, real valued function on 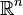 is the
support function of a nonempty compact convex set. Several proofs are known
,[3]
one is using the fact that the Legendre transform of a positive homogeneous, convex, real valued function
is the (convex) indicator function of a compact convex set.
is the
support function of a nonempty compact convex set. Several proofs are known
,[3]
one is using the fact that the Legendre transform of a positive homogeneous, convex, real valued function
is the (convex) indicator function of a compact convex set.
Many authors restrict the support function to the Euclidean unit sphere
and consider it as a function on Sn-1.
The homogeneity property shows that this restriction determines the
support function on 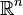 , as defined above.
, as defined above.
As a function of A
The support functions of a dilated or translated set are closely related to the original set A:
and
The latter generalises to
where A + B denotes the Minkowski sum:
The Hausdorff distance d H(A, B) of two nonempty compact convex sets A and B can be expressed in terms of support functions,
where, on the right hand side, the uniform norm on the unit sphere is used.
The properties of the support function as a function of the set A are sometimes summarized in saying
that  :A
:A 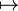 h A maps the family of non-empty
compact convex sets to the cone of all real-valued continuous functions on the sphere whose positive
homogeneous extension is convex. Abusing terminology slightly,
h A maps the family of non-empty
compact convex sets to the cone of all real-valued continuous functions on the sphere whose positive
homogeneous extension is convex. Abusing terminology slightly,  is sometimes called linear, as it respects Minkowski addition, although it is not
defined on a linear space, but rather on an (abstract) convex cone of nonempty compact convex sets.
The mapping
is sometimes called linear, as it respects Minkowski addition, although it is not
defined on a linear space, but rather on an (abstract) convex cone of nonempty compact convex sets.
The mapping  is an isometry between this cone, endowed with the Hausdorff metric, and
a subcone of the family of continuous functions on Sn-1 with the uniform norm.
is an isometry between this cone, endowed with the Hausdorff metric, and
a subcone of the family of continuous functions on Sn-1 with the uniform norm.
Variants
In contrast to the above, support functions are sometimes defined on the boundary of A rather than on Sn-1, under the assumption that there exists a unique exterior unit normal at each boundary point. Convexity is not needed for the definition. For an oriented regular surface, M, with a unit normal vector, N, defined everywhere on its surface, the support function is then defined by
-
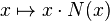 .
.
In other words, for any 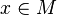 , this support function gives the
signed distance of the unique hyperplane that touches M in x.
, this support function gives the
signed distance of the unique hyperplane that touches M in x.
See also
References
- ↑ T. Bonnesen, W. Fenchel, Theorie der konvexen Körper, Julius Springer, Berlin, 1934. English translation: Theory of convex bodies, BCS Associates, Moscow, ID, 1987.
- ↑ R. J. Gardner, Geometric tomography, Cambridge University Press, New York, 1995. Second edition: 2006.
- ↑ 3.0 3.1 R. Schneider, Convex bodies: the Brunn-Minkowski theory, Cambridge University Press, Cambridge, 1993.