Superstrong cardinal

In mathematics, a cardinal number κ is called superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and 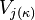$V_{j(\kappa)}$ ⊆ M.

Similarly, a cardinal κ is n-superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and 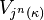$V_{j^n(\kappa)}$ ⊆ M. Akihiro Kanamori has shown that the consistency strength of an n+1-superstrong cardinal exceeds that of an n-huge cardinal for each n > 0.

References

Kanamori, Akihiro (2003). The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed ed.). Springer. ISBN 3-540-00384-3.