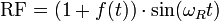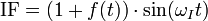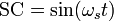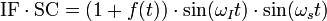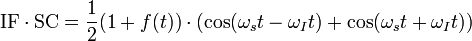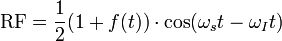Superheterodyne transmitter

Superheterodyne transmitter is a radio or TV transmitter which uses an intermediate frequency signal in addition to radio frequency signal.

Types of transmitters

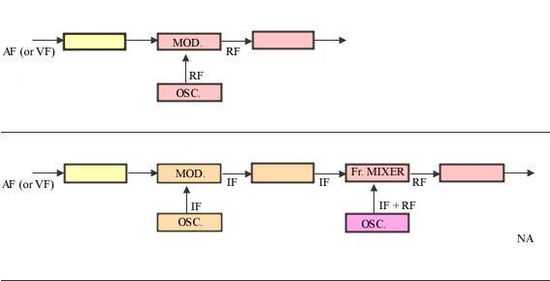
Above: Direct modulation, below superheterodyne transmitter

There are two types of transmitters. In some transmitters, the information signal (audio (AF), video (VF) etc.) modulates the radio frequency (RF) signal. These direct modulation transmitters are relatively simple transmitters.

In more complicated transmitters which are called superheterodyne, the information signal modulates an intermediate frequency (IF) signal. After stages for correction, equalization and sometimes amplification, the IF signal is converted to an RF signal by a stage named frequency mixer or frequency converter. Superheterodyne transmitters are more complex than direct modulation transmitters.

Mathematical approach

Let

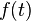$f (t)$ be the information signal

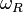$\omega_{R}$ be the angular RF,

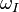$\omega_{I}$ be the angular IF and

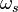$\omega_{s}$ be the angular subcarrier frequency.

In direct modulation transmitter the information signal modulates the RF carrier. If the type of modulation is conventional amplitude modulation the RF output is,

\mbox{RF}=(1+f(t))\cdot \sin(\omega_{R} t)

Likewise in superheterodyne transmitter the modulated IF is;

\mbox{IF}=(1+f(t))\cdot \sin(\omega_{I} t)

This signal is applied to a frequency mixer. The other input to the mixer is a high frequency subcarrier signal.

$\mbox{SC}= \sin( \omega_{s} t)$

The two signals are multiplied to give;

\mbox{IF}\cdot \mbox{SC}=(1+f(t))\cdot \sin(\omega_{I} t)\cdot \sin(\omega_{s} t)

Applying well known rules of trigonometry;

\mbox{IF}\cdot \mbox{SC}= \frac{1}{2}(1+f(t))\cdot (\cos(\omega_{s} t-\omega_{I} t)+\cos(\omega_{s}t +\omega_{I} t))

A filter at the output of the mixer filters out one of the terms at the right (usually the summation) leaving RF

\mbox{RF}= \frac{1}{2}(1+f(t)) \cdot \cos(\omega_{s} t-\omega_{I} t)

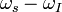Here $\omega_{s}-\omega_{I}$ is the required angular RF; i.e.,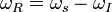 $\omega_R= \omega_{s}-\omega_{I}$

After phase and amplitude equalization,

\mbox{RF}=(1+f(t))\cdot \sin(\omega_{R} t)

Advantages of superheterodyne

In transmitters several correction and equalization stages are used after modulation. In direct modulation these stages must be developed separatelly for each output RF (so called channel). On the other hand, in superheterodyne transmitters since a single intermediate frequency signal is used, only one type of stage for IF is developed. Thus the said stages are more reliable in superheterodyne. Also R&D is much easier for the designer.

Operators may change the RF output of the transmitter. In direct modulation, it is very difficult to change the RF output. Because in this case, practically all stages need to be retuned for the new RF. On the other hand in superheterodyne only the output stages need to be retuned.

With a fast enough DAC, the modulated IF signal can be generated directly, digitally from a microprocessor or a digital signal processor. This will permit usage of more advanced methods of modulation without the use of complicated modulator hardware, and make software defined radio possible.

Analog television broadcasting topics

Systems	180-line 405-line ( System A ) 441-line 525-line ( System J , System M ) 625-line ( System B , System C , System D , System G , System H , System I , System K , System N ) 819-line ( System E , System F )

Color systems	NTSC PAL PAL-M PAL-S PALplus SECAM

Video	Back porch and front porch Black level Blanking level Chrominance Chrominance subcarrier Colorburst Color killer Color TV Composite video Frame (video) Horizontal scan rate Horizontal blanking interval Luma Nominal analogue blanking Overscan Raster scan Safe area Television lines Vertical blanking interval White clipper

Sound	Multichannel television sound NICAM Sound-in-Syncs Zweikanalton

Modulation	Frequency modulation Quadrature amplitude modulation Vestigial sideband modulation (VSB)

Transmission	Amplifiers Antenna (radio) Broadcast transmitter/Transmitter station Cavity amplifier Differential gain Differential phase Diplexer Dipole antenna Dummy load Frequency mixer Intercarrier method Intermediate frequency Output power of an analog TV transmitter Pre-emphasis Residual carrier Split sound system Superheterodyne transmitter Television receive-only Direct-broadcast satellite television Television transmitter Terrestrial television Transposer

Frequencies & Bands	Frequency offset Microwave transmission Television channel frequencies UHF VHF

Propagation	Beam tilt Distortion Earth bulge Field strength in free space Knife-edge effect Noise (electronics) Null fill Path loss Radiation pattern Skew Television interference

Testing	Distortionmeter Field strength meter Vectorscope VIT signals Zero reference pulse

Artifacts	Dot crawl Ghosting Hanover bars Sparklies

Superheterodyne transmitter

Types of transmitters

Mathematical approach

Advantages of superheterodyne

See also