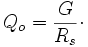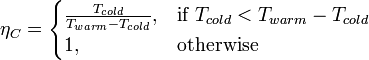Superconducting radio frequency

The Cornell storage ring 500 MHz SRF cavity.

Superconducting radio frequency (SRF) science and technology involves the application of electrical superconductors to radio frequency devices. The ultra-low electrical resistivity of a superconducting material allows an RF resonator to obtain an extremely high quality factor, Q. For example, it is commonplace for a 1.3 GHz niobium SRF resonant cavity at 1.8 Kelvin to obtain a quality factor of Q=5×1010. Such a very high Q resonator stores energy with very low loss and narrow bandwidth. These properties can be exploited for a variety of applications, including the construction of high-performance particle accelerator structures.

Introduction

The amount of loss in an SRF resonant cavity is so minute that it is often explained with the following comparison: Galileo Galilei (1564–1642) was one of the first investigators of pendulous motion, a simple form of mechanical resonance. Had Galileo experimented with a 1 Hz resonator with a quality factor Q typical of today's SRF cavities and left it swinging in a sepulchered lab since the early 17th century, that pendulum would still be swinging today with about half of its original amplitude.

Photograph of the Cornell storage ring 500 MHz SRF cavity being lifted out of a cryogenic test dewar while still cold.

The most common application of superconducting RF is in particle accelerators. Accelerators typically use resonant RF cavities formed from or coated with superconducting materials. Electromagnetic fields are excited in the cavity by coupling in an RF source with an antenna. When the RF frequency fed by the antenna is the same as that of a cavity mode, the resonant fields build to high amplitudes. Charged particles passing through apertures in the cavity are then accelerated by the electric fields and deflected by the magnetic fields. The resonant frequency driven in SRF cavities typically ranges from 200 MHz to 3 GHz, depending on the particle species to be accelerated.

The most common fabrication technology for such SRF cavities is to form thin walled (1–3 mm) shell components from high purity niobium sheets by stamping. These shell components are then welded together to form cavities. Several such finished products are pictured below.

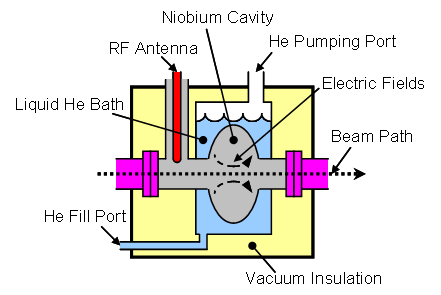
A simplified diagram of the key elements of an SRF cavity setup is shown below. The cavity is immersed in a saturated liquid helium bath. Pumping removes helium vapor boil-off and controls the bath temperature. The helium vessel is often pumped to a pressure below helium's superfluid lambda point to take advantage of the superfluid's thermal properties. Because superfluid has very high thermal conductivity, it makes an excellent coolant. In addition, superfluids boil only at free surfaces, preventing the formation of bubbles on the surface of the cavity, which would cause mechanical perturbations. An antenna is needed in the setup to couple RF power to the cavity fields and, in turn, any passing particle beam. The cold portions of the setup need to be extremely well insulated, which is best accomplished by a vacuum vessel surrounding the helium vessel and all ancillary cold components. The full SRF cavity containment system, including the vacuum vessel and many details not discussed here, is a cryomodule.

Entry into superconducting RF technology can incur more complexity, expense, and time than normal-conducting RF cavity strategies. SRF requires chemical facilities for harsh cavity treatments, a low-particulate cleanroom for high-pressure water rinsing and assembly of components, and complex engineering for the cryomodule vessel and cryogenics. A vexing aspect of SRF is the as-yet elusive ability to consistently produce high Q cavities in high volume production, which would be required for a large linear collider. Nevertheless, for many applications the capabilities of SRF cavities provide the only solution for a host of demanding performance requirements.

Several extensive treatments of SRF physics and technology are available, many of them free of charge and online. There are the proceedings of CERN accelerator schools,[1][2][3] a scientific paper giving a thorough presentation of the many aspects of an SRF cavity to be used in the International Linear Collider,[4] bi-annual International Conferences on RF Superconductivity held at varying global locations in odd numbered years,[5] and tutorials presented at the conferences.[6]

A collection of SRF cavities developed at Cornell University with frequencies spanning 200 MHz to 3 GHz.

SRF cavity application in particle accelerators

A large variety of RF cavities are used in particle accelerators. Historically most have been made of copper – a good electrical conductor – and operated near room temperature with water cooling (cooling is necessary to remove the heat generated by the electrical loss in the cavity). In the past two decades, however, accelerator facilities have increasingly found superconducting cavities to be more suitable (or necessary) for their accelerators than normal-conducting copper versions. The motivation for using superconductors in RF cavities is not to achieve a net power savings, but rather to increase the "quality" of the beam attunement. Though superconductors have very small electrical resistance, the little power they do dissipate is radiated at very low temperatures, typically in a liquid helium bath at 1.6 K to 4.5 K, and maintaining such low temperatures takes a lot of energy. The refrigeration power to maintain the cryogenic bath at low temperature in the presence of heat from small RF power dissipation is dictated by the Carnot efficiency, and can easily be comparable to the normal-conductor power dissipation of a room-temperature copper cavity. The principal motivations for using superconducting RF cavities, are:

When future advances in superconducting material science allow higher superconducting critical temperatures Tc and consequently higher SRF bath temperatures, then the reduced thermocline between the cavity and the surrounding environment could yield a significant net power savings by SRF over the normal conducting approach to RF cavities. Other issues will need to be considered with a higher bath temperature, though, such as the fact that superfluidity (which is presently exploited with liquid helium) would not be present with (for example) liquid nitrogen. At present, none of the "high Tc" superconducting materials are suitable for RF applications. Shortcomings of these materials arise due to their underlying physics as well as their bulk mechanical properties not being amenable to fabricating accelerator cavities. However, depositing films of promising materials onto other mechanically amenable cavity materials may provide a viable option for exotic materials serving SRF applications. At present, the de facto choice for SRF material is still pure niobium, which has a critical temperature of 9.3 K and functions as a superconductor nicely in a liquid helium bath of 4.2 K or lower.

Physics of SRF cavities

The physics of Superconducting RF can be complex and lengthy. A few simple approximations derived from the complex theories, though, can serve to provide some of the important parameters of SRF cavities.

By way of background, some of the pertinent parameters of RF cavities are itemized as follows. A resonator's quality factor is defined by

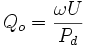Q_o = \frac{\omega U} {P_d} ,

where:

ω is the resonant frequency in [rad/s],
U is the energy stored in [J], and
Pd is the power dissipated in [W] in the cavity to maintain the energy U.

The energy stored in the cavity is given by the integral of field energy density over its volume,

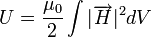U = \frac{\mu_0}{2}\int{|\overrightarrow{H}|^2 dV} ,

where:

H is the magnetic field in the cavity and
μ0 is the permeability of free space.

The power dissipated is given by the integral of resistive wall losses over its surface,

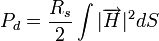P_d = \frac{R_s}{2}\int{|\overrightarrow{H}|^2 dS} ,

where:

Rs is the surface resistance which will be discussed below.

The integrals of the electromagnetic field in the above expressions are generally not solved analytically, since the cavity boundaries rarely lie along axes of common coordinate systems. Instead, the calculations are performed by any of a variety of computer programs that solve for the fields for non-simple cavity shapes, and then numerically integrate the above expressions.

An RF cavity parameter known as the Geometry Factor ranks the cavity's effectiveness of providing accelerating electric field due to the influence of its shape alone, which excludes specific material wall loss. The Geometry Factor is given by

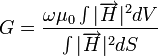G = \frac{\omega \mu_0 \int{|\overrightarrow{H}|^2 dV}}{\int{|\overrightarrow{H}|^2 dS}} ,

and then

Q_o = \frac{G} {R_s} \cdot

The geometry factor is quoted for cavity designs to allow comparison to other designs independent of wall loss, since wall loss for SRF cavities can vary substantially depending on material preparation, cryogenic bath temperature, electromagnetic field level, and other highly variable parameters. The Geometry Factor is also independent of cavity size, it is constant as a cavity shape is scaled to change its frequency.

As an example of the above parameters, a typical 9-cell SRF cavity for the International Linear Collider[4] (a.k.a. a TESLA cavity) would have G=270 Ω and Rs= 10 nΩ, giving Qo=2.7×1010.

The critical parameter for SRF cavities in the above equations is the surface resistance Rs, and is where the complex physics comes into play. For normal-conducting copper cavities operating near room temperature, Rs is simply determined by the empirically measured bulk electrical conductivity σ by

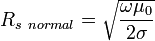R_{s\ normal} = \sqrt{ \frac{\omega \mu_0} {2 \sigma} } .

For copper at 300 K, σ=5.8×107 (Ω·m)−1 and at 1.3 GHz, Rs copper= 9.4 mΩ.

For Type II superconductors in RF fields, Rs can be viewed as the sum of the superconducting BCS resistance and temperature-independent "residual resistances",

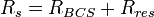R_s = R_{BCS} + R_{res} .

The BCS resistance derives from BCS theory. One way to view the nature of the BCS RF resistance is that the superconducting Cooper pairs, which have zero resistance for DC current, have finite mass and momentum which has to alternate sinusoidally for the AC currents of RF fields, thus giving rise to a small energy loss. The BCS resistance for niobium can be approximated when the temperature is less than half of niobium's superconducting critical temperature, T<Tc/2, by

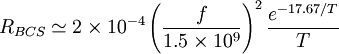R_{BCS} \simeq 2 \times 10^{-4} \left( \frac{f}{1.5 \times 10^{9}} \right)^2 \frac {e^{-17.67 / T}} {T} [Ω],

where:

f is the frequency in [Hz],
T is the temperature in [K], and
Tc=9.3 K for niobium, so this approximation is valid for T<4.65 K.

Note that for superconductors, the BCS resistance increases quadratically with frequency, ~f 2, whereas for normal conductors the surface resistance increases as the root of frequency, ~√f. For this reason, the majority of superconducting cavity applications favor lower frequencies, <3 GHz, and normal-conducting cavity applications favor higher frequencies, >0.5 GHz, there being some overlap depending on the application.

The superconductor's residual resistance arises from several sources, such as random material defects, hydrides that can form on the surface due to hot chemistry and slow cool-down, and others that are yet to be identified. One of the quantifiable residual resistance contributions is due to an external magnetic field pinning magnetic fluxons in a Type II superconductor. The pinned fluxon cores create small normal-conducting regions in the niobium that can be summed to estimate their net resistance. For niobium, the magnetic field contribution to Rs can be approximated by

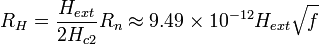R_{H} = \frac{H_{ext}}{2 H_{c2}} R_n \approx 9.49 \times 10^{-12} H_{ext}\sqrt{f} [Ω],

where:

Hext is any external magnetic field in [Oe],
Hc2 is the Type II superconductor magnetic quench field, which is 2400 Oe (190 kA/m) for niobium, and
Rn is the normal-conducting resistance of niobium in ohms.

The Earth's nominal magnetic flux of 0.5 gauss (50 µT) translates to a magnetic field of 0.5 Oe (40 A/m) and would produce a residual surface resistance in a superconductor that is orders of magnitude greater than the BCS resistance, rendering the superconductor too lossy for practical use. For this reason, superconducting cavities are surrounded by magnetic shielding to reduce the field permeating the cavity to typically <10 mOe (0.8 A/m).

Using the above approximations for a niobium a SRF cavity at 1.8 K, 1.3 GHz, and assuming a magnetic field of 10 mOe (0.8 A/m), the surface resistance components would be

RBCS = 4.55 nΩ and
Rres = RH = 3.42 nΩ, giving a net surface resistance
Rs = 7.97 nΩ. If for this cavity
G = 270 Ω then the ideal quality factor would be
Qo = 3.4×1010.

The Qo just described can be further improved by up to a factor of 2 by performing a mild vacuum bake of the cavity. Empirically, the bake seems to reduce the BCS resistance by 50%, but increases the residual resistance by 30%. The plot below shows the ideal Qo values for a range of residual magnetic field for a baked and unbaked cavity.

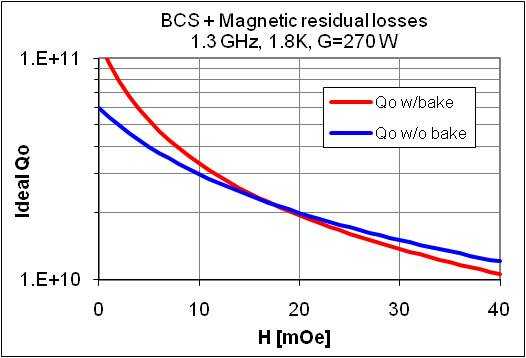
In general, much care and attention to detail must be exercised in the experimental setup of SRF cavities so that there is not Qo degradation due to RF losses in ancillary components, such as stainless steel vacuum flanges that are too close to the cavity's evanescent fields. However, careful SRF cavity preparation and experimental configuration have achieved the ideal Qo not only for low field amplitudes, but up to cavity fields that are typically 75% of the magnetic field quench limit. Few cavities make it to the magnetic field quench limit since residual losses and vanishingly small defects heat up localized spots, which eventually exceed the superconducting critical temperature and lead to a thermal quench.

Q vs E

When using superconducting RF cavities in particle accelerators, the field level in the cavity should generally be as high as possible to most efficiently accelerate the beam passing through it. The Qo values described by the above calculations tend to degrade as the fields increase, which is plotted for a given cavity as a "Q vs E" curve, where "E" refers to the accelerating electric field of the TM01 mode. Ideally, the cavity Qo would remain constant as the accelerating field is increased all the way up to the point of a magnetic quench field, as indicated by the "ideal" dashed line in the plot below. In reality, though, even a well prepared niobium cavity will have a Q vs E curve that lies beneath the ideal, as shown by the "good cavity" curve in the plot.

There are many phenomena that can occur in an SRF cavity to degrade its Q vs E performance, such as impurities in the niobium, hydrogen contamination due to excessive heat during chemistry, and a rough surface finish. After a couple decades of development, a necessary prescription for successful SRF cavity production is emerging. This includes:

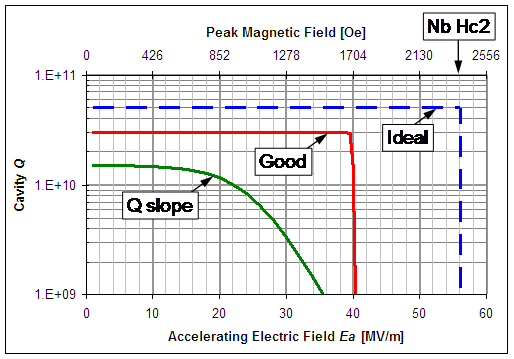
There remains some uncertainty as to the root cause of why some of these steps lead to success, such as the electropolish and vacuum bake. However, if this prescription is not followed, the Q vs E curve often shows an excessive degradation of Qo with increasing field, as shown by the "Q slope" curve in the plot below. Finding the root causes of Q slope phenomena is the subject of ongoing fundamental SRF research. The insight gained could lead to simpler cavity fabrication processes as well as benefit future material development efforts to find higher Tc alternatives to niobium.

Wakefields and higher order modes (HOMs)

One of the main reasons for using SRF cavities in particle accelerators is that their large apertures result in low beam impedance and higher thresholds of deleterious beam instabilities. As a charged particle beam passes through a cavity, its electromagnetic radiation field is perturbed by the sudden increase of the conducting wall diameter in the transition from the small-diameter beampipe to the large hollow RF cavity. A portion of the particle's radiation field is then "clipped off" upon re-entrance into the beampipe and left behind as wakefields in the cavity. The wakefields are simply superimposed upon the externally driven accelerating fields in the cavity. The spawning of electromagnetic cavity modes as wakefields from the passing beam is analogous to a drumstick striking a drumhead and exciting many resonant mechanical modes.

The beam wakefields in an RF cavity excite a subset of the spectrum of the many electromagnetic modes, including the externally driven TM01 mode. There are then a host of beam instabilities that can occur as the repetitive particle beam passes through the RF cavity, each time adding to the wakefield energy in a collection of modes.

For a particle bunch with charge q, a length much shorter than the wavelength of a given cavity mode, and traversing the cavity at time t=0, the amplitude of the wakefield voltage left behind in the cavity in a given mode is given by[7]

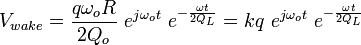V_{wake} = \frac{q \omega_o R} {2 Q_o} \ e^{j \omega_o t} \ e^{-\frac{\omega t}{2 Q_L}} = k q \ e^{j \omega_o t} \ e^{-\frac{\omega t}{2 Q_L}} ,

where:

R is the shunt impedance of the cavity mode defined by
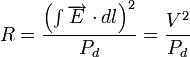R = \frac{ \left( \int{\overrightarrow{E} \cdot dl} \right)^2}{P_d} = \frac{V^2}{P_d} ,
E is the electric field of the RF mode,
Pd is the power dissipated in the cavity to produce the electric field E,
QL is the "loaded Q" of the cavity, which takes into account energy leakage out of the coupling antenna,
ωo is the angular frequency of the mode,
the imaginary exponential is the mode's sinusoidal time variation,
the real exponential term quantifies the decay of the wakefield with time, and
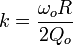k = \frac{\omega_o R} {2 Q_o} is termed the loss parameter of the RF mode.

The shunt impedance R can be calculated from the solution of the electromagnetic fields of a mode, typically by a computer program that solves for the fields. In the equation for Vwake, the ratio R/Qo serves as a good comparative measure of wakefield amplitude for various cavity shapes, since the other terms are typically dictated by the application and are fixed. Mathematically,

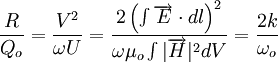\frac{R} {Q_o} = \frac{V^2}{\omega U} = \frac{2 \left( \int{\overrightarrow{E} \cdot dl} \right)^2}{ \omega \mu_o\int{|\overrightarrow{H}|^2 dV} } = \frac {2k}{\omega_o} ,

where relations defined above have been used. R/Qo is then a parameter that factors out cavity dissipation and is viewed as measure of the cavity geometry's effectiveness of producing accelerating voltage per stored energy in its volume. The wakefield being proportional to R/Qo can be seen intuitively since a cavity with small beam apertures concentrates the electric field on axis and has high R/Qo, but also clips off more of the particle bunch's radiation field as deleterious wakefields.

The calculation of electromagnetic field buildup in a cavity due to wakefields can be complex and depends strongly on the specific accelerator mode of operation. For the straightforward case of a storage ring with repetitive particle bunches spaced by time interval Tb and a bunch length much shorter than the wavelength of a given mode, the long term steady state wakefield voltage presented to the beam by the mode is given by[7]

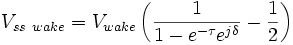V_{ss \ wake} = V_{wake} \left( \frac{1} {1 - e^{-\tau} e^{j\delta}} - \frac{1}{2} \right) ,

where:

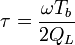\tau = \frac{\omega T_b}{2 Q_L} is the decay of the wakefield between bunches, and
δ is the phase shift of the wakefield mode between bunch passages through the cavity.

As an example calculation, let the phase shift δ=0, which would be close to the case for the TM01 mode by design and unfortunately likely to occur for a few HOM's. Having δ=0 (or an integer multiple of an RF mode's period, δ=n2π) gives the worse-case wakefield build-up, where successive bunches are maximally decelerated by previous bunches' wakefields and give up even more energy than with only their "self wake". Then, taking ω = 2π 500 MHz, Tb=1 µs, and QL=106, the buildup of wakefields would be Vss wake=637×Vwake. A pitfall for any accelerator cavity would be the presence of what is termed a "trapped mode". This is an HOM that does not leak out of the cavity and consequently has a QL that can be orders of magnitude larger than used in this example. In this case, the buildup of wakefields of the trapped mode would likely cause a beam instability. The beam instability implications due to the Vss wake wakefields is thus addressed differently for the fundamental accelerating mode TM01 and all other RF modes, as described next.

Fundamental accelerating mode TM01

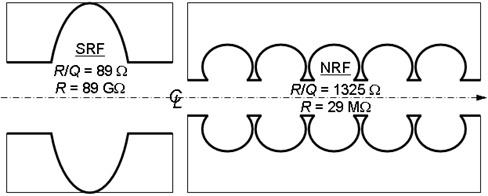
The complex calculations treating wakefield-related beam stability for the TM01 mode in accelerators show that there are specific regions of phase between the beam bunches and the driven RF mode that allow stable operation at the highest possible beam currents. At some point of increasing beam current, though, just about any accelerator configuration will become unstable. As pointed out above, the beam wakefield amplitude is proportional to the cavity parameter R/Qo, so this is typically used as a comparative measure of the likelihood of TM01 related beam instabilities. A comparison of R/Qo and R for a 500 MHz superconducting cavity and a 500 MHz normal-conducting cavity is shown below. The accelerating voltage provided by both cavities is comparable for a given net power consumption when including refrigeration power for SRF. The R/Qo for the SRF cavity is 15 times less than the normal-conducting version, and thus less beam-instability susceptible. This one of the main reasons such SRF cavities are chosen for use in high-current storage rings.

Higher order modes (HOMs)

Photograph of the Cornell electron storage ring beamline HOM load.

In addition to the fundamental accelerating TM01 mode of an RF cavity, numerous higher frequency modes and a few lower-frequency dipole modes are excited by charged particle beam wakefields, all generally denoted higher order modes (HOMs). These modes serve no useful purpose for accelerator particle beam dynamics, only giving rise to beam instabilities, and are best heavily damped to have as low a QL as possible. The damping is accomplished by preferentially allowing dipole and all HOMs to leak out of the SRF cavity, and then coupling them to resistive RF loads. The leaking out of undesired RF modes occurs along the beampipe, and results from a careful design of the cavity aperture shapes. The aperture shapes are tailored to keep the TM01 mode "trapped" with high Qo inside of the cavity and allow HOMs to propagate away. The propagation of HOMs is sometimes facilitated by having a fluted beampipe on one side of the cavity, as seen in the SRF cavity photograph at the top of this wiki page. The flutes present an effectively larger beampipe diameter to asymmetric RF modes, allowing them to easily propagate away from the cavity, while presenting an effectively small diameter to the axisymmetric TM01 mode and hindering its propagation.

The resistive load for HOMs can be implemented by having loop antennas located at apertures on the side of the beampipe, with coaxial lines routing the RF to outside of the cryostat to standard RF loads. Another approach is to place the HOM loads directly on the beampipe as hollow cylinders with RF lossy material attached to the interior surface, as shown in the image to the right. This "beamline load" approach can be more technically challenging, since the load must absorb high RF power while preserving a high-vacuum beamline environment in close proximity to a contamination-sensitive SRF cavity. Further, such loads must sometimes operate at cryogenic temperatures to avoid large thermal gradients along the beampipe from the cold SRF cavity. The benefit of the beamline HOM load configuration, however, is a greater absorptive bandwidth and HOM attenuation as compared to antenna coupling. This benefit can be the difference between a stable vs. an unstable particle beam for high current accelerators.

Cryogenics

Main article: Cryomodule

A significant part of SRF technology is cryogenic engineering. The SRF cavities tend to be thin-walled structures immersed in a bath of liquid helium having temperature 1.6 K to 4.5 K. Careful engineering is then required to insulate the helium bath from the room-temperature external environment. This is accomplished by:

The major cryogenic engineering challenge is the refrigeration plant for the liquid helium. The small power that is dissipated in an SRF cavity and the heat leak to the vacuum vessel are both heat loads at very low temperature. The refrigerator must replenish this loss with an inherent poor efficiency, given by the product of the Carnot efficiency ηC and a "practical" efficiency ηp. The Carnot efficiency derives from the second law of thermodynamics and can be quite low. It is given by

\eta_C = \begin{cases} \frac{T_{cold}} {T_{warm} - T_{cold}}, & \mbox{if } T_{cold} < T_{warm} - T_{cold} \\ 1, & \mbox{otherwise} \end{cases}

where

Tcold is the temperature of the cold load, which is the helium vessel in this case, and
Twarm is the temperature of the refrigeration heat sink, usually room temperature.

In most cases Twarm =300 K, so for Tcold ≥150 K the Carnot efficiency is unity. The practical efficiency is a catch-all term that accounts for the many mechanical non-idealities that come into play in a refrigeration system aside from the fundamental physics of the Carnot efficiency. For a large refrigeration installation there is some economy of scale, and it is possible to achieve ηp in the range of 0.2–0.3. The wall-plug power consumed by the refrigerator is then

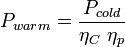P_{warm} = \frac{P_{cold}} {\eta_C \ \eta_{p}} ,

where

Pcold is the power dissipated at temperature Tcold .

As an example, if the refrigerator delivers 1.8 K helium to the cryomodule where the cavity and heat leak dissipate Pcold=10 W, then the refrigerator having Twarm=300 K and ηp=0.3 would have ηC=0.006 and a wall-plug power of Pwarm=5.5 kW. Of course, most accelerator facilities have numerous SRF cavities, so the refrigeration plants can get to be very large installations.

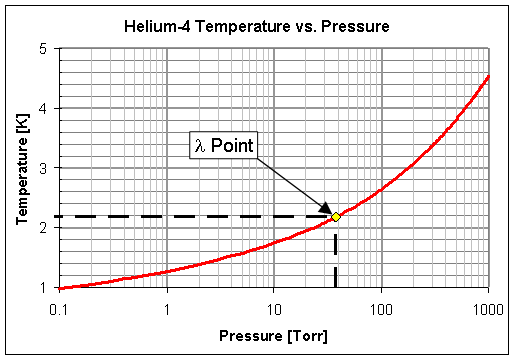
The temperature of operation of an SRF cavity is typically selected as a minimization of wall-plug power for the entire SRF system. The plot to the right then shows the pressure to which the helium vessel must be pumped to obtain the desired liquid helium temperature. Atmospheric pressure is 760 Torr (101.325 kPa), corresponding to 4.2 K helium. The superfluid λ point occurs at about 38 Torr (5.1 kPa), corresponding to 2.18 K helium. Most SRF systems either operate at atmospheric pressure, 4.2 K, or below the λ point at a system efficiency optimum usually around 1.8 K, corresponding to about 12 Torr (1.6 kPa).

References