Sun Zhiwei

Zhi-Wei Sun (Chinese: 孙智伟; pinyin: Sūn Zhìwěi; Wade–Giles: Sun Chihwei, born October 16, 1965) is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University.

Born in Huai'an, Jiangsu, Sun and his twin brother Sun Zhihong proved a theorem about what are now known as the Wall-Sun-Sun primes that guided the search for counterexamples to Fermat's last theorem.

In 2003, he presented a unified approach to three famous topics of Paul Erdős in combinatorial number theory: covering systems, restricted sumsets, and zero-sum problems or EGZ Theorem.[1]

He used q-series to prove that any natural number can be represented as a sum of an even square and two triangular numbers. He conjectured, and proved with B.-K. Oh, that each positive integer can be represented as a sum of a square, an odd square and a triangular number.[2] In 2009, he conjectured that any natural number can be written as the sum of two squares and a pentagonal number, as the sum of a triangular number, an even square and a pentagonal number, and as the sum of a square, a pentagonal number and a hexagonal number.[3] He also raised many open conjectures on congruences [4] and posed over 100 conjectural series for powers of 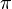\pi.[5]

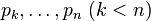In 2013 he published a paper [6] containing many conjectures on primes one of which states that for any positive integer m there are consecutive primes p_k,\ldots,p_n\ (k<n) not exceeding 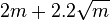2m+2.2\sqrt{m} such that 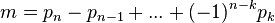m=p_n-p_{n-1}+...+(-1)^{n-k}p_k, where 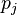p_j denotes the 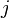j-th prime.

His Erdős number is 2. He is the Editor-in-Chief of Journal of Combinatorics and Number Theory.

See also

Notes

  1. ↑ \Z
  2. ↑ Mixed sums of squares and triangular numbers (III)
  3. ↑ On universal sums of polygonal numbers
  4. ↑ Open conjectures on congruences
  5. ↑ \pi
  6. ↑ On functions taking only prime values, J. Number Theory 133(2013), 2794-2812

External links