Summability kernel

In mathematics, a summability kernel is a family or sequence of periodic integrable functions satisfying a certain set of properties, listed below. Certain kernels, such as the Fejér kernel, are particularly useful in Fourier analysis. Summability kernels are related to approximation of the identity; definitions of an approximation of identity vary,^[1] but sometimes the definition of an approximation of the identity is taken to be the same as for a summability kernel.

Definition

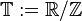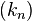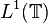Let $\mathbb{T}:=\mathbb{R}/\mathbb{Z}$ . A summability kernel is a sequence $(k_n)$ in $L^1(\mathbb{T})$ that satisfies

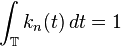
$\int_\mathbb{T}k_n(t)\,dt=1$
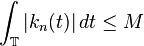$\int_\mathbb{T}|k_n(t)|\,dt\le M$ (uniformly bounded)
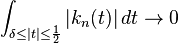$\int_{\delta\le|t|\le\frac{1}{2}}|k_n(t)|\,dt\to0$ as $n\to\infty$ , for every $\delta>0$ .

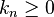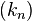Note that if $k_n\ge0$ for all $n$ , i.e. $(k_n)$ is a positive summability kernel, then the second requirement follows automatically from the first.

If instead we take the convention 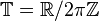$\mathbb{T}=\mathbb{R}/2\pi\mathbb{Z}$ , the first equation becomes 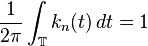$\frac{1}{2\pi}\int_\mathbb{T}k_n(t)\,dt=1$ , and the upper limit of integration on the third equation should be extended to $\pi$ .

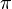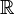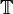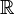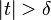We can also consider $\mathbb{R}$ rather than $\mathbb{T}$ ; then we integrate (1) and (2) over $\mathbb{R}$ , and (3) over $|t|>\delta$ .

Examples

The Fejér kernel
The Poisson kernel (continuous index)
The Dirichlet kernel is not a summability kernel, since it fails the second requirement.

Convolutions

Let 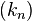$(k_n)$ be a summability kernel, and $*$ denote the convolution operation.

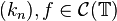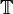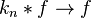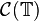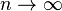If $(k_n),f\in\mathcal{C}(\mathbb{T})$ (continuous functions on $\mathbb{T}$ ), then $k_n*f\to f$ in $\mathcal{C}(\mathbb{T})$ , i.e. uniformly, as $n\to\infty$ .
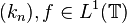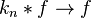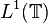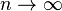If $(k_n),f\in L^1(\mathbb{T})$ , then $k_n*f\to f$ in $L^1(\mathbb{T})$ , as $n\to\infty$ .
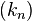If $(k_n)$ is radially decreasing symmetric and 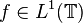$f\in L^1(\mathbb{T})$ , then 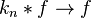$k_n*f\to f$ pointwise a.e., as 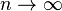$n\to\infty$ . This uses the Hardy–Littlewood maximal function. If 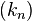$(k_n)$ is not radially decreasing symmetric, but the decreasing symmetrization 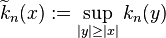$\widetilde{k}_n(x):=\sup_{|y|\ge|x|}k_n(y)$ satisfies 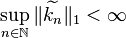$\sup_{n\in\mathbb{N}}\|\widetilde{k_n}\|_1<\infty$ , then a.e. convergence still holds, using a similar argument.

References

↑ http://math.stackexchange.com/questions/114028/approximation-of-the-identity-and-hardy-littlewood-maximal-function

Katznelson, Yitzhak (2004), An introduction to Harmonic Analysis, Cambridge University Press, ISBN 0-521-54359-2