Sullivan conjecture
In mathematics, Sullivan conjecture can refer to any of several results and conjectures prompted by homotopy theory work of Dennis Sullivan. A basic theme and motivation concerns the fixed point set in group actions of a finite group  . The most elementary formulation, however, is in terms of the classifying space
. The most elementary formulation, however, is in terms of the classifying space 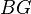 of such a group. Roughly speaking, it is difficult to map such a space
of such a group. Roughly speaking, it is difficult to map such a space 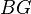 continuously into a finite CW complex
continuously into a finite CW complex  in a non-trivial manner. Such a version of the Sullivan conjecture was first proved by Haynes Miller.[1] Specifically, in 1984, Miller proved that the function space, carrying the compact-open topology, of base point-preserving mappings from
in a non-trivial manner. Such a version of the Sullivan conjecture was first proved by Haynes Miller.[1] Specifically, in 1984, Miller proved that the function space, carrying the compact-open topology, of base point-preserving mappings from 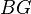 to
to  is weakly contractible.
is weakly contractible.
This is equivalent to the statement that the map  →
→ 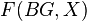 from X to the function space of maps
from X to the function space of maps 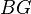 →
→  , not necessarily preserving the base point, given by sending a point
, not necessarily preserving the base point, given by sending a point  of
of  to the constant map whose image is
to the constant map whose image is  is a weak equivalence. The mapping space
is a weak equivalence. The mapping space 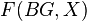 is an example of a homotopy fixed point set. Specifically,
is an example of a homotopy fixed point set. Specifically, 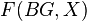 is the homotopy fixed point set of the group
is the homotopy fixed point set of the group  acting by the trivial action on
acting by the trivial action on  . In general, for a group
. In general, for a group  acting on a space
acting on a space  , the homotopy fixed points are the fixed points
, the homotopy fixed points are the fixed points 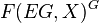 of the mapping space
of the mapping space 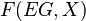 of maps from the universal cover
of maps from the universal cover 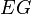 of
of 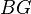 to
to  under the
under the  -action on
-action on 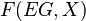 given by
given by  in
in  acts on a map
acts on a map  in
in 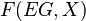 by sending it to
by sending it to 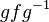 . The
. The  -equivariant map from
-equivariant map from 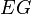 to a single point
to a single point  induces a natural map η:
induces a natural map η: 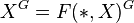 →
→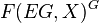 from the fixed points to the homotopy fixed points of
from the fixed points to the homotopy fixed points of  acting on
acting on  . Miller's theorem is that η is a weak equivalence for trivial
. Miller's theorem is that η is a weak equivalence for trivial  -actions on finite-dimensional CW complexes. An important ingredient and motivation (see [1]) for his proof is a result of Gunnar Carlsson on the homology of
-actions on finite-dimensional CW complexes. An important ingredient and motivation (see [1]) for his proof is a result of Gunnar Carlsson on the homology of 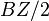 as an unstable module over the Steenrod algebra.[2]
as an unstable module over the Steenrod algebra.[2]
Miller's theorem generalizes to a version of Sullivan's conjecture in which the action on  is allowed to be non-trivial. In,[3] Sullivan conjectured that η is a weak equivalence after a certain p-completion procedure due to A. Bousfield and D. Kan for the group
is allowed to be non-trivial. In,[3] Sullivan conjectured that η is a weak equivalence after a certain p-completion procedure due to A. Bousfield and D. Kan for the group 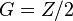 . This conjecture was incorrect as stated, but a correct version was given by Miller, and proven independently by Dwyer-Miller-Neisendorfer,[4] Carlsson,[5] and Jean Lannes,[6] showing that the natural map
. This conjecture was incorrect as stated, but a correct version was given by Miller, and proven independently by Dwyer-Miller-Neisendorfer,[4] Carlsson,[5] and Jean Lannes,[6] showing that the natural map 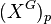 →
→ 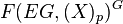 is a weak equivalence when the order of
is a weak equivalence when the order of  is a power of a prime p, and where
is a power of a prime p, and where 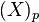 denotes the Bousfield-Kan p-completion of
denotes the Bousfield-Kan p-completion of  . Miller's proof involves an unstable Adams spectral sequence, Carlsson's proof uses his affirmative solution of the Segal conjecture and also provides information about the homotopy fixed points
. Miller's proof involves an unstable Adams spectral sequence, Carlsson's proof uses his affirmative solution of the Segal conjecture and also provides information about the homotopy fixed points 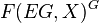 before completion, and Lannes's proof involves his T-functor.[7]
before completion, and Lannes's proof involves his T-functor.[7]
References
- ↑ Haynes Miller, The Sullivan Conjecture on Maps from Classifying Spaces, The Annals of Mathematics, second series, Vol. 120 No. 1, 1984, pp. 39-87. JSTOR: The Annals of Mathematics. Accessed May 9, 2012.
- ↑ Carlsson, Gunnar (1983). "G.B. Segal's Burnside Ring Conjecture for (Z/2)^k". Topology 22 (1): 83–103. doi:10.1016/0040-9383(83)90046-0.
- ↑ Sullivan, Denis (1971). Geometric topology. Part I. Cambridge, MA: Massachusetts Institute of Technology Press. p. 432.
- ↑ Dwyer, William; Haynes Miller; Joseph Neisendorfer (1989). "Fibrewise Completion and Unstable Adams Spectral Sequences". Israel Journal of Mathematics 66 (1-3). doi:10.1007/bf02765891.
- ↑ Carlsson, Gunnar (1991). "Equivariant stable homotopy and Sullivan's conjecture". Invent. math. 103: 497–525. doi:10.1007/bf01239524.
- ↑ Lannes, Jean (1992). "Sur les espaces fonctionnels dont la source est le classifiant d'un p-groupe abélien élémentaire". Publications Mathématiques de l'I.H.E.S. 75: 135–244. doi:10.1007/bf02699494.
- ↑ Schwartz, Lionel (1994). Unstable Modules over the Steenrod Algebra and Sullivan's Fixed Point Set Conjecture. Chicago and London: The University of Chicago Press. ISBN 0-226-74203-2.
External links
- Gottlieb, Daniel H. (2001), "Sullivan conjecture", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Book extract
- J. Lurie's course notes