Submodular set function
In mathematics, a submodular set function (also known as a submodular function) is a set function whose value, informally, has the property that the difference in the value of the function that a single element makes when added to an input set decreases as the size of the input set increases. Submodular functions have a natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory (as functions modeling user preferences), electrical networks, and very recently, in Machine Learning and Artificial Intelligence.
Definition
If 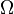 is a set, a submodular function is a set function
is a set, a submodular function is a set function 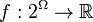 , where
, where 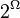 denotes the power set of
denotes the power set of 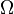 , which satisfies one of the following equivalent definitions.[1]
, which satisfies one of the following equivalent definitions.[1]
- For every
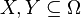 with
with 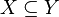 and every
and every 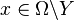 we have that
we have that 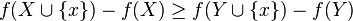 .
. - For every
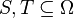 we have that
we have that 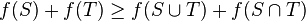 .
. - For every
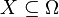 and
and 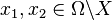 we have that
we have that 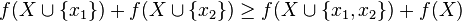 .
.
A nonnegative submodular function is also a subadditive function, but a subadditive function need not be submodular.
Types of submodular functions
Monotone
A submodular function  is monotone if for every
is monotone if for every 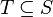 we have that
we have that 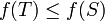 . Examples of monotone submodular functions include:
. Examples of monotone submodular functions include:
- Linear functions
- Any function of the form
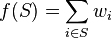 is called a linear function. Additionally if
is called a linear function. Additionally if 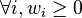 then f is monotone.
then f is monotone. - Budget-additive functions
- Any function of the form
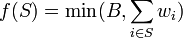 for each
for each 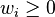 and
and 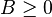 is called budget additive.
is called budget additive. - Coverage functions
- Let
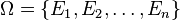 be a collection of subsets of some ground set
be a collection of subsets of some ground set 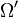 . The function
. The function 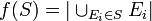 for
for 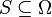 is called a coverage function. This can be generalized by adding non-negative weights to the elements.
is called a coverage function. This can be generalized by adding non-negative weights to the elements. - Entropy
- Let
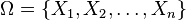 be a set of random variables. Then for any
be a set of random variables. Then for any 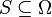 we have that
we have that 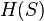 is a submodular function, where
is a submodular function, where 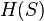 is the entropy of the set of random variables
is the entropy of the set of random variables 
- Matroid rank functions
- Let
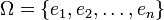 be the ground set on which a matroid is defined. Then the rank function of the matroid is a submodular function.[2]
be the ground set on which a matroid is defined. Then the rank function of the matroid is a submodular function.[2]
Non-monotone
A submodular function which is not monotone is called non-monotone.
Symmetric
A non-monotone submodular function  is called symmetric if for every
is called symmetric if for every 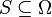 we have that
we have that 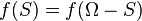 .
Examples of symmetric non-monotone submodular functions include:
.
Examples of symmetric non-monotone submodular functions include:
- Graph cuts
- Let
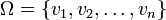 be the vertices of a graph. For any set of vertices
be the vertices of a graph. For any set of vertices 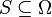 let
let 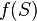 denote the number of edges
denote the number of edges 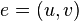 such that
such that 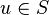 and
and 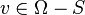 . This can be generalized by adding non-negative weights to the edges.
. This can be generalized by adding non-negative weights to the edges. - Mutual information
- Let
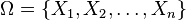 be a set of random variables. Then for any
be a set of random variables. Then for any 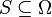 we have that
we have that 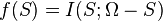 is a submodular function, where
is a submodular function, where 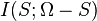 is the mutual information.
is the mutual information.
Asymmetric
A non-monotone submodular function which is not symmetric is called asymmetric.
- Directed cuts
- Let
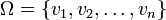 be the vertices of a directed graph. For any set of vertices
be the vertices of a directed graph. For any set of vertices 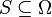 let
let 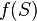 denote the number of edges
denote the number of edges 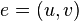 such that
such that 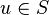 and
and 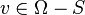 . This can be generalized by adding non-negative weights to the directed edges.
. This can be generalized by adding non-negative weights to the directed edges.
Continuous extensions
Lovász extension
This extension is named after mathematician László Lovász. Consider any vector 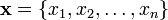 such that each
such that each 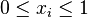 . Then the Lovász extension is defined as
. Then the Lovász extension is defined as 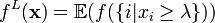 where the expectation is over
where the expectation is over  chosen from the uniform distribution on the interval
chosen from the uniform distribution on the interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) . The Lovász extension is a convex function.
. The Lovász extension is a convex function.
Multilinear extension
Consider any vector 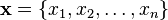 such that each
such that each 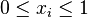 . Then the multilinear extension is defined as
. Then the multilinear extension is defined as 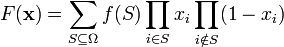 .
.
Convex closure
Consider any vector 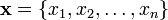 such that each
such that each 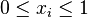 . Then the convex closure is defined as
. Then the convex closure is defined as 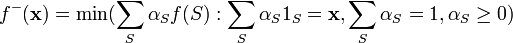 . It can be shown that
. It can be shown that 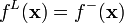 .
.
Concave closure
Consider any vector 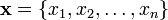 such that each
such that each 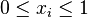 . Then the concave closure is defined as
. Then the concave closure is defined as 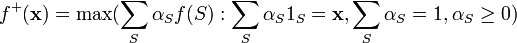 .
.
Properties
- The class of submodular functions is closed under non-negative linear combinations. Consider any submodular function
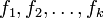 and non-negative numbers
and non-negative numbers 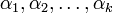 . Then the function
. Then the function  defined by
defined by 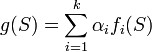 is submodular. Furthermore, for any submodular function
is submodular. Furthermore, for any submodular function  , the function defined by
, the function defined by 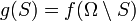 is submodular. The function
is submodular. The function 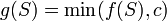 , where
, where  is a real number, is submodular whenever
is a real number, is submodular whenever  is monotonic.
is monotonic. - If
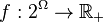 is a submodular function then
is a submodular function then 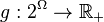 defined as
defined as 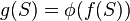 where
where  is a concave function, is also a submodular function.
is a concave function, is also a submodular function. - Consider a random process where a set
 is chosen with each element in
is chosen with each element in 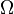 being included in
being included in  independently with probability
independently with probability  . Then the following inequality is true
. Then the following inequality is true ![\mathbb{E}[f(T)]\geq p f(\Omega)+(1-p) f(\varnothing)](../I/m/d056f419d7bba33450fed73d9d2a2603.png) where
where 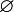 is the empty set. More generally consider the following random process where a set
is the empty set. More generally consider the following random process where a set  is constructed as follows. For each of
is constructed as follows. For each of 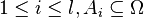 construct
construct  by including each element in
by including each element in 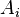 independently into
independently into  with probability
with probability 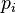 . Furthermore let
. Furthermore let 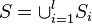 . Then the following inequality is true
. Then the following inequality is true ![\mathbb{E}[f(S)]\geq \sum_{R\subseteq [l]} \Pi_{i\in R}p_i \Pi_{i\notin R}(1-p_i)f(\cup_{i\in R}A_i)](../I/m/f61b463802fdaf6a848d11529332e268.png) .
.
Optimization problems
Submodular functions have properties which are very similar to convex and concave functions. For this reason, an optimization problem which concerns optimizing a convex or concave function can also be described as the problem of maximizing or minimizing a submodular function subject to some constraints.
Submodular Minimization
The simplest minimization problem is to find a set 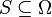 which minimizes a submodular function subject to no constraints. This problem is computable in (strongly)[3][4] polynomial time.[5][6] Computing the minimum cut in a graph is a special case of this general minimization problem. Unfortunately, however, even simple constraints like cardinality lower bound constraints make this problem NP hard, with polynomial lower bound approximation factors.[7][8]
which minimizes a submodular function subject to no constraints. This problem is computable in (strongly)[3][4] polynomial time.[5][6] Computing the minimum cut in a graph is a special case of this general minimization problem. Unfortunately, however, even simple constraints like cardinality lower bound constraints make this problem NP hard, with polynomial lower bound approximation factors.[7][8]
Submodular Maximization
Unlike minimization, maximization of submodular functions is usually NP-hard. Many problems, such as max cut and the maximum coverage problem, can be cast as special cases of this general maximization problem under suitable constraints. Typically, the approximation algorithms for these problems are based on either greedy algorithms or local search algorithms. The problem of maximizing a symmetric non-monotone submodular function subject to no constraints admits a 1/2 approximation algorithm.[9] Computing the maximum cut of a graph is a special case of this problem. The more general problem of maximizing an arbitrary non-monotone submodular function subject to no constraints also admits a 1/2 approximation algorithm.[10] The problem of maximizing a monotone submodular function subject to a cardinality constraint admits a 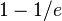 approximation algorithm.[11] The maximum coverage problem is a special case of this problem. The more general problem of maximizing a monotone submodular function subject to a matroid constraint also admits a
approximation algorithm.[11] The maximum coverage problem is a special case of this problem. The more general problem of maximizing a monotone submodular function subject to a matroid constraint also admits a 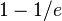 approximation algorithm.[12][13] Many of these algorithms can be unified within a semi-differential based framework of algorithms.[8]
approximation algorithm.[12][13] Many of these algorithms can be unified within a semi-differential based framework of algorithms.[8]
Related Optimization Problems
Apart from submodular minimization and maximization, another natural problem is Difference of Submodular Optimization.[14][15] Unfortunately, this problem is not only NP hard, but also inapproximable.[15] A related optimization problem is minimize or maximize a submodular function, subject to a submodular level set constraint (also called submodular optimization subject to submodular cover or submodular knapsack constraint). This problem admits bounded approximation guarantees.[16] Another optimization problem involves partitioning data based on a submodular function, so as to maximize the average welfare. This problem is called the submodular welfare problem.[17]
Applications
Submodular functions naturally occur in several real world applications, in Economics, Game Theory, Machine Learning and Computer Vision. Owing the diminishing returns property, submodular functions naturally model costs of items, since there is often a larger discount, with an increase in the items one buys. Submodular functions model notions of complexity, similarity and cooperation when the appear in minimization problems. In maximization problems, on the other hand, they model notions of diversity, information and coverage. For more information on applications of submodularity, particularly in machine learning, see [18][19][20]
See also
Citations
- ↑ (Schrijver 2003, §44, p. 766)
- ↑ Fujishige (2005) p.22
- ↑ S. Iwata, L. Fleischer, and S. Fujishige, A combinatorial strongly polynomial algorithm for minimizing submodular functions, J. ACM 48 (2001), pp. 761–777.
- ↑ A. Schrijver, A combinatorial algorithm minimizing submodular functions in strongly polynomial time, J. Combin. Theory Ser. B 80 (2000), pp. 346–355.
- ↑ M. Grötschel, L. Lovasz and A. Schrijver, The ellipsoid method and its consequences in combinatorial optimization, Combinatorica 1 (1981), pp. 169–197.
- ↑ W. H. Cunningham, On submodular function minimization, Combinatorica,5 (1985),pp. 185–192.
- ↑ Z. Svitkina and L. Fleischer, Submodular approximation: Sampling-based algorithms and lower bounds, SIAM Journal of Computing (2011).
- ↑ 8.0 8.1 R. Iyer, S. Jegelka and J. Bilmes, Fast Semidifferential based submodular function optimization, Proc. ICML (2013).
- ↑ U. Feige, V. Mirrokni and J. Vondrák, Maximizing non-monotone submodular functions, Proc. of 48th FOCS (2007), pp. 461–471.
- ↑ N. Buchbinder, M. Feldman, J. Naor and R. Schwartz, A tight linear time (1/2)-approximation for unconstrained submodular maximization, Proc. of 53rd FOCS (2012), pp. 649-658.
- ↑ G. L. Nemhauser, L. A. Wolsey and M. L. Fisher, An analysis of approximations for maximizing submodular set functions I, Mathematical Programming 14 (1978), 265–294.
- ↑ G. Calinescu, C. Chekuri, M. Pál and J. Vondrák, Maximizing a submodular set function subject to a matroid constraint, SIAM J. Comp. 40:6 (2011), 1740-1766.
- ↑ Y. Filmus, J. Ward, A tight combinatorial algorithm for submodular maximization subject to a matroid constraint, Proc. of 53rd FOCS (2012), pp. 659-668.
- ↑ M. Narasimhan and J. Bilmes, A submodular-supermodular procedure with applications to discriminative structure learning, In Proc. UAI (2005).
- ↑ 15.0 15.1 R. Iyer and J. Bilmes, Algorithms for Approximate Minimization of the Difference between Submodular Functions, In Proc. UAI (2012).
- ↑ R. Iyer and J. Bilmes, Submodular Optimization Subject to Submodular Cover and Submodular Knapsack Constraints, In Advances of NIPS (2013).
- ↑ J. Vondrák, Optimal approximation for the submodular welfare problem in the value oracle model, Proc. of STOC (2008), pp. 461–471.
- ↑ http://submodularity.org/.
- ↑ A. Krause and C. Guestrin, Beyond Convexity: Submodularity in Machine Learning, Tutorial at ICML-2008
- ↑ J. Bilmes, Submodularity in Machine Learning Applications, Tutorial at AAAI-2015
References
- Schrijver, Alexander (2003), Combinatorial Optimization, Springer, ISBN 3-540-44389-4
- Lee, Jon (2004), A First Course in Combinatorial Optimization, Cambridge University Press, ISBN 0-521-01012-8
- Fujishige, Satoru (2005), Submodular Functions and Optimization, Elsevier, ISBN 0-444-52086-4
- Narayanan, H. (1997), Submodular Functions and Electrical Networks, ISBN 0-444-82523-1
- Oxley, James G. (1992), Matroid theory, Oxford Science Publications, Oxford: Oxford University Press, ISBN 0-19-853563-5, Zbl 0784.05002
External links
- http://www.cs.berkeley.edu/~stefje/references.html has a longer bibliography