Subdivided interval categories

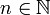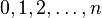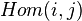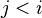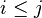In category theory (mathematics) there exists an important collection of categories denoted $[n]$ for natural numbers $n\in\mathbb{N}$ . The objects of $[n]$ are the integers $0,1,2,\ldots,n$ , and the morphism set $Hom(i,j)$ for objects $i,j\in[n]$ is empty if $j<i$ and consists of a single element if $i\leq j$ .

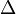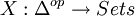Subdivided interval categories are very useful in defining simplicial sets. The category whose objects are the subdivided interval categories and whose morphisms are functors is often written $\Delta$ and is called the simplicial indexing category. A simplicial set is just a contravariant functor $X:\Delta^{op}\rightarrow Sets$ .

Examples

The category 𝟘 is an empty interval, that is, an empty category, having any objects or morphisms. It is an initial object in the category of all categories.

The category [0], also denoted as 𝟙, is a one-object, one-morphism category. It is the terminal object in the category of all categories.

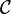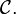
The category [1], also denoted as 𝟚 has two objects and a single (non-identity) morphism between them. If $\mathcal{C}$ is any category, then $\mathcal{C}^{[1]}$ is the category of morphisms and commutative squares in $\mathcal{C}.$

The category [2], also denoted as 𝟛 has three objects and three non-identity morphisms.

References

MacLane, S. Categories for the working mathematician.