Subadditive set function
In mathematics, a subadditive set function is a set function whose value, informally, has the property that the value of function on the union of two sets is at most the sum of values of the function on each of the sets. This is thematically related to the subadditivity property of real-valued functions.
Definition
If 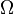 is a set, a subadditive function is a set function
is a set, a subadditive function is a set function 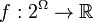 , where
, where 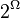 denotes the power set of
denotes the power set of 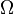 , which satisfies the following inequality.[1][2]
, which satisfies the following inequality.[1][2]
For every 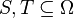 we have that
we have that 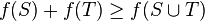 .
.
Examples of subadditive functions
1. Every non-negative submodular set function is subadditive (the family of submodular functions is strictly contained in the family of subadditive functions).
2. Functions based on set cover. Let 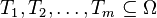 such that
such that 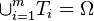 . Then
. Then  is defined as the minimum number of subsets required to cover a given set:
is defined as the minimum number of subsets required to cover a given set:
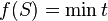 such that there exists sets
such that there exists sets 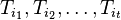 satisfying
satisfying 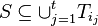 .
.
3. The maximum of additive set functions is subadditive (Dually, the minimum of additive functions is superadditive). Formally, let for each 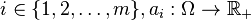 be linear (additive) set functions. Then
be linear (additive) set functions. Then 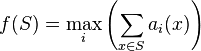 is a subadditive set function.
is a subadditive set function.
4. Fractionally subadditive set functions. This is a generalization of submodular function and special case of subadditive function. If 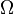 is a set, a fractionally subadditive function is a set function
is a set, a fractionally subadditive function is a set function  , where
, where 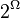 denotes the power set of
denotes the power set of 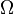 , which satisfies the following definition:[1]
, which satisfies the following definition:[1]
- For every
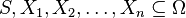 such that
such that 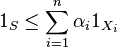 then we have that
then we have that 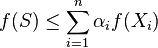 .
. - This definition is equivalent to the definition of the maximum in 3 above.[1]
Properties
- If
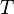 is a set chosen such that each
is a set chosen such that each 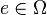 is included into
is included into 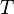 with probability
with probability 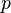 then the following inequality is satisfied
then the following inequality is satisfied ![\mathbb{E}[f(T)]\geq p f(\Omega)](../I/m/7d0d4fad34061cb970ed219635d38421.png) .
.
See also
Citations