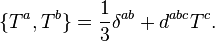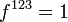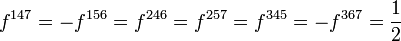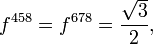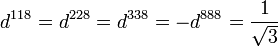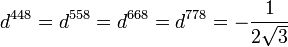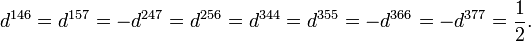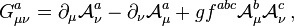Structure constants
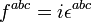 , where
, where 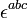 is the completely antisymmetric tensor.
is the completely antisymmetric tensor.In group theory, a discipline within mathematics, the structure constants of a Lie group determine the commutation relations between its generators in the associated Lie algebra.
Definition
Given a set of generators 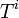 , the structure constants
, the structure constants 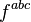 express the Lie brackets of pairs of generators as linear combinations of generators from the set, i.e.
express the Lie brackets of pairs of generators as linear combinations of generators from the set, i.e.
![[T^a, T^b] = f^{abc} T^c](../I/m/6265cfd131f980b6c1d7ed0b407cbecf.png) .
.
The structure constants determine the Lie brackets of elements of the Lie algebra, and consequently nearly completely determine the group structure of the Lie group. For small elements 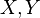 of the Lie algebra, the structure of the Lie group near the identity element is given by
of the Lie algebra, the structure of the Lie group near the identity element is given by ![\exp(X)\exp(Y) \approx \exp(X + Y + \tfrac{1}{2}[X,Y])](../I/m/e205748a4799129e30c7fd6911b890f2.png) . This expression is made exact by the Baker–Campbell–Hausdorff formula.
. This expression is made exact by the Baker–Campbell–Hausdorff formula.
Examples
SU(2)
This algebra is three-dimensional, with generators given by the Pauli matrices 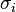 . The generators of the group SU(2) satisfy the commutation relations (where
. The generators of the group SU(2) satisfy the commutation relations (where 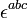 is the Levi-Civita symbol):
is the Levi-Civita symbol):
In this case, 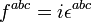 , and the distinction between upper and lower indexes doesn't matter (the metric is the Kronecker delta
, and the distinction between upper and lower indexes doesn't matter (the metric is the Kronecker delta 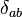 ).
).
This lie algebra is isomorphic to the lie algebra of SO(3),and also to the Clifford algebra of ℝ3, called the algebra of physical space.
SU(3)
A less trivial example is given by SU(3):
Its generators, T, in the defining representation, are:
where 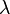 , the Gell-Mann matrices, are the SU(3) analog of the Pauli matrices for SU(2):
, the Gell-Mann matrices, are the SU(3) analog of the Pauli matrices for SU(2):
These obey the relations
The structure constants are given by:
and all other 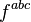 not related to these by permutation are zero.
not related to these by permutation are zero.
The d take the values:
Hall polynomials
The Hall polynomials are the structure constants of the Hall algebra.
Applications
- A lie group is abelian exactly when all structure constants are 0.
- A lie group is real exactly when its structure constants are real.
- A nilpotent Lie group admits a lattice if and only if its Lie algebra admits a basis with rational structure constants: this is Malcev's criterion. Not all nilpotent Lie groups admit lattices; for more details, see also Raghunathan.[1]
- In quantum chromodynamics, the symbol
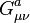 represents the gauge invariant gluon field strength tensor, analogous to the electromagnetic field strength tensor, Fμν, in quantum electrodynamics. It is given by:[2]
represents the gauge invariant gluon field strength tensor, analogous to the electromagnetic field strength tensor, Fμν, in quantum electrodynamics. It is given by:[2]
- where fabc are the structure constants of SU(3). Note that the rules to push-up or pull-down the a, b, or c indexes are trivial, (+,... +), so that fabc = fabc = fa
bc whereas for the μ or ν indexes one has the non-trivial relativistic rules, corresponding e.g. to the metric signature (+ − − −).
References
- ↑ Raghunathan, Chapter II, Discrete Subgroups of Lie Groups, M. S. Raghunathan
- ↑ M. Eidemüller, H.G. Dosch, M. Jamin (1999). "The field strength correlator from QCD sum rules". Nucl.Phys.Proc.Suppl.86:421-425,2000 (Heidelberg, Germany). arXiv:hep-ph/9908318.
- Weinberg, Steven, The Quantum Theory of Fields, Volume 1: Foundations, Cambridge University Press, Cambridge, (1995). ISBN 0-521-55001-7.
![[\sigma_a, \sigma_b] = i \epsilon^{abc} \sigma_c \,](../I/m/b6e405c99ffee191f5fd0a36829a98ee.png)
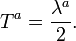
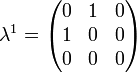
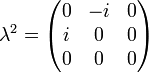
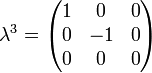
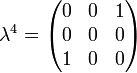
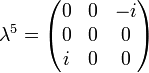
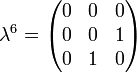
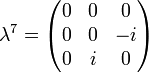
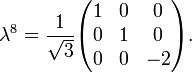
![\left[T^a, T^b \right] = i f^{abc} T^c \,](../I/m/4e352b83119d48de78cdba89991fffe0.png)