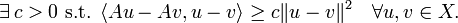Strongly monotone

In functional analysis, an operator 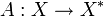$A:X\to X^*$ where X is a real Hilbert space is said to be strongly monotone if

\exists\,c>0 \mbox{ s.t. } \langle Au-Av , u-v \rangle\geq c \|u-v\|^2 \quad \forall u,v\in X.

This is analogous to the notion of strictly increasing for scalar-valued functions of one scalar argument.

See also

Monotonic function

References

Zeidler. Applied Functional Analysis (AMS 108) p. 173