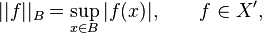Strong topology (polar topology)
In functional analysis and related areas of mathematics the strong topology is the finest polar topology, the topology with the most open sets, on a dual pair. The coarsest polar topology is called weak topology.
Definition
Let  be a dual pair of vector spaces over the field
be a dual pair of vector spaces over the field  of real (
of real (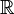 ) or complex (
) or complex (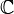 ) numbers. Let us denote by
) numbers. Let us denote by 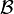 the system of all subsets
the system of all subsets 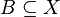 bounded by elements of
bounded by elements of  in the following sense:
in the following sense:
Then the strong topology  on
on  is defined as the locally convex topology on
is defined as the locally convex topology on  generated by the seminorms of the form
generated by the seminorms of the form
In the special case when  is a locally convex space, the strong topology on the (continuous) dual space
is a locally convex space, the strong topology on the (continuous) dual space 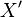 (i.e. on the space of all continuous linear functionals
(i.e. on the space of all continuous linear functionals 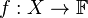 ) is defined as the strong topology
) is defined as the strong topology 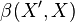 , and it coincides with the topology of uniform convergence on bounded sets in
, and it coincides with the topology of uniform convergence on bounded sets in  , i.e. with the topology on
, i.e. with the topology on 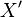 generated by the seminorms of the form
generated by the seminorms of the form
where  runs over the family of all bounded sets in
runs over the family of all bounded sets in  . The space
. The space 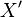 with this topology is called strong dual space of the space
with this topology is called strong dual space of the space  and is denoted by
and is denoted by 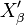 .
.
Examples
- If
 is a normed vector space, then its (continuous) dual space
is a normed vector space, then its (continuous) dual space 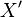 with the strong topology coincides with the Banach dual space
with the strong topology coincides with the Banach dual space 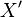 , i.e. with the space
, i.e. with the space  with the topology induced by the operator norm. Conversely
with the topology induced by the operator norm. Conversely  -topology on
-topology on  is identical to the topology induced by the norm on
is identical to the topology induced by the norm on  .
.
Properties
- If
 is a barrelled space, then its topology coincides with the strong topology
is a barrelled space, then its topology coincides with the strong topology  on
on  and with the Mackey topology on
and with the Mackey topology on  generated by the pairing
generated by the pairing  .
.
References
- Schaefer, Helmuth H. (1966). Topological vector spaces. New York: The MacMillan Company. ISBN 0-387-98726-6.
| ||||||||||||||||||||||||||||||||||