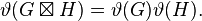Strong product of graphs
In graph theory, the strong product G ⊠ H of graphs G and H is a graph such that
- the vertex set of G ⊠ H is the Cartesian product V(G) × V(H); and
- any two distinct vertices (u,u') and (v,v') are adjacent in G × H if and only if:
- u is adjacent to v and u'=v', or
- u=v and u' is adjacent to v', or
- u is adjacent to v and u' is adjacent to v'
The strong product is also called the normal product and AND product. It was first introduced by Sabidussi in 1960.
Shannon capacity and Lovász number
The Shannon capacity of a graph is defined from the independence number of its strong products with itself, by the formula
László Lovász showed that Lovász theta function is multiplicative:[1]
He used this fact to upper bound the Shannon capacity by the Lovász number.
See also
Notes
- ↑ See Lemma 2 and Theorem 7 in Lovász (1979).
References
- Imrich, Wilfried; Klavžar, Sandi; Rall, Douglas F. (2008). Graphs and their Cartesian Products. A. K. Peters. ISBN 1-56881-429-1.
- Lovász, László (1979), "On the Shannon Capacity of a Graph", IEEE Transactions on Information Theory, IT-25 (1).
- Sabidussi, G. (1960). "Graph multiplication". Math. Z. 72: 446–457. doi:10.1007/BF01162967. MR 0209177.
![\Theta(G)
= \sup_k \sqrt[k]{\alpha(G^k)}
= \lim_{k \rightarrow \infty} \sqrt[k]{\alpha(G^k)},](../I/m/fe076c7f83a2cb6fc42ec9b26c7e1e86.png)