Strong duality
Strong duality is a concept in optimization such that the primal and dual solutions are equivalent. This is as opposed to weak duality (the primal problem has optimal value greater than the dual problem, in other words the duality gap is positive).
Characterizations
Strong duality holds if and only if the duality gap is equal to 0.
Sufficient conditions
-
where 
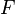is the perturbation function relating the primal and dual problems and 
is the biconjugate of 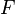; - the primal problem is a linear optimization problem;
- Slater's condition for a convex optimization problem.[1][2]
See also
References
- ↑ Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 978-0-387-29570-1.
- ↑ Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 3, 2011.