Strong coloring
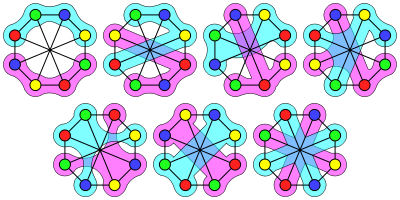
In graph theory, a strong coloring, with respect to a partition of the vertices into (disjoint) subsets of equal sizes, is a (proper) vertex coloring in which every color appears exactly once in every partition. When the order of the graph G is not divisible by k, we add isolated vertices to G just enough to make the order of the new graph G′ divisible by k. In that case, a strong coloring of G′ minus the previously added isolated vertices is considered a strong coloring of G. A graph is strongly k-colorable if, for each partition of the vertices into sets of size k, it admits a strong coloring.
The strong chromatic number sχ(G) of a graph G is the least k such that G is strongly k-colorable. A graph is strongly k-chromatic if it has strong chromatic number k.
Some properties of sχ(G):
- sχ(G) > Δ(G).
- sχ(G) ≤ 3 Δ(G) − 1 (Haxell)
- Asymptotically, sχ(G) ≤ 11 Δ(G) / 4 + o(Δ(G)). (Haxell)
Here Δ(G) is the maximum degree.
Strong chromatic number was independently introduced by Alon (1988) and Fellows (1990).
References
- Alon, Noga (1988). "The linear arboricity of a graph". Israel J. Math. 62 (3): 311–325. doi:10.1007/BF02783300.
- Alon, Noga (1992). "The strong chromatic number". Random Structures and Algorithms 3: 1–7. doi:10.1002/rsa.3240030102.
- Fellows, Michael R. (1990). "Transversals of vertex partition in graphs". SIAM Journal on Discrete Mathematics 3 (2): 206–215. doi:10.1137/0403018.
- Haxell, P.E. (2004). "On the strong chromatic number". Combinatorics, Probability and Computing 13: 857–865. doi:10.1017/S0963548304006157.
- Jensen, Tommy R.; Toft, Bjarne (1995). Graph coloring problems. New York: Wiley-Interscience. ISBN 0-471-02865-7.