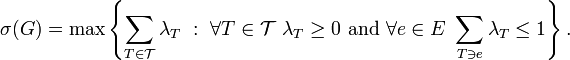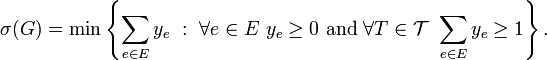Strength of a graph
| Strength of a graph: example | |
|---|---|
|
A graph with strength 2: the graph is here decomposed into three parts, with 4 edges between the parts, giving a ratio of 4/(3-1)=2. | |
In the branch of mathematics called graph theory, the strength of an undirected graph corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions of the set of vertices and detect zones of high concentration of edges.
Definitions
The strength  of an undirected simple graph G = (V, E) admits the three following definitions:
of an undirected simple graph G = (V, E) admits the three following definitions:
- Let
 be the set of all partitions of
be the set of all partitions of  , and
, and 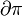 be the set of edges crossing over the sets of the partition
be the set of edges crossing over the sets of the partition 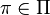 , then
, then 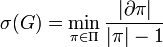 .
. - Also if
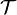 is the set of all spanning trees of G, then
is the set of all spanning trees of G, then
- And by linear programming duality,
Complexity
Computing the strength of a graph can be done in polynomial time, and the first such algorithm
was discovered by Cunningham (1985). The algorithm with best complexity for computing exactly the strength is due to Trubin (1993), uses the flow decomposition of Goldberg and Rao (1998), in time 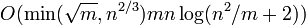 .
.
Properties
- If
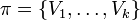 is one partition that maximizes, and for
is one partition that maximizes, and for 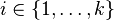 ,
, 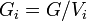 is the restriction of G to the set
is the restriction of G to the set 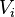 , then
, then 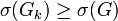 .
.
- The Tutte-Nash-Williams theorem:
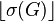 is the maximum number of edge-disjoint spanning trees that can be contained in G.
is the maximum number of edge-disjoint spanning trees that can be contained in G.
- Contrary to the graph partition problem, the partitions output by computing the strength are not necessarily balanced (i.e. of almost equal size).
References
- W. H. Cunningham. Optimal attack and reinforcement of a network, J of ACM, 32:549–561, 1985.
- A. Schrijver. Chapter 51. Combinatorial Optimization, Springer, 2003.
- V. A. Trubin. Strength of a graph and packing of trees and branchings,, Cybernetics and Systems Analysis, 29:379–384, 1993.