Stratifold

In differential topology, a branch of mathematics, a stratifold is a generalization of a differentiable manifold where certain kinds of singularities are allowed. More specifically a stratifold is stratified into differentiable manifolds of (possibly) different dimensions. Stratifolds can be used to construct new homology theories. For example, they provide a new geometric model for ordinary homology. The concept of stratifolds was invented by Matthias Kreck. The basic idea is similar to that of a topologically stratified space, but adapted to differential topology.

Definitions

Before we come to stratifolds, we define a preliminary notion, which captures the minimal notion for a smooth structure on a space: A differential space (in the sense of Sikorski) is a pair (X, C), where X is a topological space and C is a subalgebra of the continuous functions $X\to\mathbb{R}$ such that a function is in C if it is locally in C and $g\circ(f_1,\dots, f_n): X\to \mathbb{R}$ is in C for $g:\mathbb{R}^n\to \mathbb{R}$ smooth and $f_i\in C$ . A simple example takes for X a smooth manifold and for C just the smooth functions.

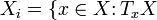For a general differential space (X, C) and a point x in X we can define as in the case of manifolds a tangent space $T_x X$ as the vector space of all derivations of function germs at x. Define strata $X_i = \{x\in X\colon T_x X$ has dimension i 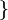$\}$ . For an n-dimensional manifold M we have that $M_n = M$ and all other strata are empty. We are now ready for the definition of a stratifold, where more than one stratum may be non-empty:

A k-dimensional stratifold is a differential space (S, C), where S is a locally compact Hausdorff space with countable base of topology. All skeleta should be closed. In addition we assume:

The suspension

The $(S_i, C|_{S_i})$ are i-dimensional smooth manifolds.
For all x in S, restriction defines an isomorphism stalks $C_x \to C^{\infty}(S_i)_x$ .
All tangent spaces have dimension ≤ k.
For each x in S and every neighbourhood U of x, there exists a function $\rho\colon U \to \R$ with $\rho(x) \neq 0$ and $\text{supp}(\rho) \subset U$ (a bump function).

A n-dimensional stratifold is called oriented if its (n − 1)-stratum is empty and its top stratum is oriented. One can also define stratifolds with boundary, the so-called c-stratifolds. One defines them as a pair $(T,\partial T)$ of topological spaces such that $T-\partial T$ is an n-dimensional stratifold and $\partial T$ is an (n − 1)-dimensional stratifold, together with an equivalence class of collars.

An important subclass of stratifolds are the regular stratifolds, which can be roughly characterized as looking locally around a point in the i-stratum like the i-stratum times a (n − i)-dimensional stratifold. This is a condition which is fulfilled in most stratifold one usually encounters.

Examples

There are plenty of examples of stratifolds. The first example to consider is the open cone over a manifold M. We define a continuous function from S to the reals to be in C iff it is smooth on M × (0, 1) and it is locally constant around the cone point. The last condition is automatic by point 2 in the definition of a stratifold. We can substitute M by a stratifold S in this construction. The cone is oriented if and only if S is oriented and not zero-dimensional. If we consider the (closed) cone with bottom, we get a stratifold with boundary S.

Other examples for stratifolds are one-point compactifications and suspensions of manifolds, (real) algebraic varieties with only isolated singularities and (finite) simplicial complexes.

Bordism theories

An example of a bordism relation

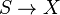In this section, we will assume all stratifolds to be regular. We call two maps $S,S' \to X$ from two oriented compact k-dimensional stratifolds into a space X bordant if there exists an oriented (k + 1)-dimensional compact stratifold T with boundary S + (−S') such that the map to X extends to T. The set of equivalence classes of such maps $S\to X$ is denoted by $SH_k X$ . The sets have actually the structure of abelian groups with disjoint union as addition. One can develop enough differential topology of stratifolds to show that these define a homology theory. 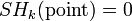Clearly, $SH_k(\text{point}) = 0$ for k > 0 since every oriented stratifold S is the boundary of its cone, which is oriented if dim(S) > 0. One can show that $SH_0(\text{point})\cong\mathbb{Z}$ . Hence, by the Eilenberg–Steenrod uniqueness theorem, $SH_k(X) \cong H_k(X)$ for every space X homotopy-equivalent to a CW-complex, where H denotes singular homology. It should be noted, however, that for other spaces these two homology theories need not be isomorphic (an example is the one-point compactification of the surface of infinite genus).

There is also a simple way to define equivariant homology with the help of stratifolds. Let G be a compact Lie group. We can then define a bordism theory of stratifolds mapping into a space X with a G-action just as above, only that we require all stratifolds to be equipped with an orientation-preserving free G-action and all maps to be G-equivariant. Denote by $SH_k^G(X)$ the bordism classes. One can prove $SH_k^G(X)\cong H_{k-\dim(G)}^G(X)$ for every X homotopy equivalent to a CW-complex.

Connection to the theory of genera

A genus is a ring homomorphism from a bordism ring into another ring. For example the Euler characteristic defines a ring homomorphism $\Omega^O(\text{point})\to \mathbb{Z}/2[t]$ from the unoriented bordism ring and the signature defines a ring homomorphism $\Omega^{SO}(\text{point})\to \mathbb{Z}[t]$ from the oriented bordism ring. Here t has in the first case degree 1 and in the second case degree 4, since only manifolds in dimensions divisible by 4 can have non-zero signature. The left hand sides of these homomorphisms are homology theories evaluated at a point. With the help of stratifolds it is possible to construct homology theories such that the right hand sides are these homology theories evaluated at a point, the Euler homology and the Hirzebruch homology respectively.

Umkehr maps

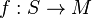Suppose, one has a closed embedding $i: N\hookrightarrow M$ of manifolds with oriented normal bundle. Then one can define an umkehr map $H_k(M)\to H_{k+\dim(N)-\dim(M)}(N)$ . One possibility is to use stratifolds: represent a class $x\in H_k(M)$ by a stratifold $f:S\to M$ . Then make ƒ transversal to N. The intersection of S and N defines a new stratifold S' with a map to N, which represents a class in $H_{k+\dim(N)-\dim(M)}(N)$ . It is possible to repeat this construction in the context of an embedding of Hilbert manifolds of finite codimension, which can be used in string topology.

References

M. Kreck, Differential Algebraic Topology: From Stratifolds to Exotic Spheres, AMS (2010), ISBN 0-8218-4898-4
The stratifold page
Euler homology