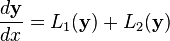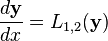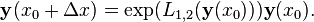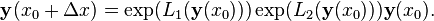Strang splitting

Strang splitting is a numerical method of solving ordinary differential equations (ODEs). It is named after Gilbert Strang. The essential idea is that a complex ODE can be decomposed into multiple simpler ODEs. Each ODE can be advanced independently, and then the total change would be the sum of all individual changes. To demonstrate this idea, suppose we have an equation of the form

\frac{d\mathbf{y}}{dx} = L_1 (\mathbf{y}) + L_2 (\mathbf{y})

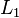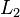where L_1, L_2 are differential operators. Suppose further that had we dropped either of the differential operators on the right hand side we would be left with equations that were much simpler to solve.

\frac{d\mathbf{y}}{dx} = L_{1,2} (\mathbf{y})

If we start from some point 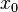x_0 where value of the function is known 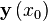\mathbf{y}\left(x_0\right) and advance it to the next point 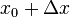x_0+\Delta x according to the simplified, reduced ODEs, we will get

\mathbf{y} (x_0+\Delta x) = \exp(L_{1,2} (\mathbf{y} (x_0))) \mathbf{y} (x_0).

Combining these two advancement operators yields the value of the function at the next point, according to the complete ODE

\mathbf{y} (x_0+\Delta x) = \exp(L_1 (\mathbf{y}(x_0))) \exp(L_2(\mathbf{y}(x_0))) \mathbf{y}(x_0).

References