Stomatal conductance

By definition, stomatal conductance, usually measured in mmol m⁻² s⁻¹, is the measure of the rate of passage of carbon dioxide (CO₂) entering, or water vapor exiting through the stomata of a leaf. Stomata are small pores on the top and bottom of a leaf that are responsible for taking in and expelling CO₂ and moisture from and to the outside air. The rate of stomatal conductance, or its inverse, stomatal resistance, is directly related to the boundary layer resistance of the leaf and the absolute concentration gradient of water vapor from the leaf to the atmosphere. It is under direct biological control of the leaf through the use of guard cells, which surround the stomatal pore ^[1] (Taiz/Zeiger 1991). Stomatal conductance is integral to leaf level calculations of transpiration (E).

Methods for Measuring

Stomatal conductance can be measured in several ways: Steady-state porometers: A steady state porometer measures stomatal conductance using a sensor head with a fixed diffusion path to the leaf. It measures the vapor concentration at two different locations in the diffusion path. It computes vapor flux from the vapor concentration measurements and the known conductance of the diffusion path using the following equation:

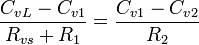
$\frac{C_{vL}-C_{v1}}{R_{vs}+R_1}=\frac{C_{v1}-C_{v2}}{R_2}$

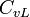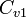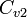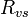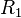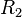Where $C_{vL}$ is the vapor concentration at the leaf, $C_{v1}$ and $C_{v2}$ are the concentrations at the two sensor locations, $R_{vs}$ is the stomatal resistance, and $R_1$ and $R_2$ are the resistances at the two sensors. If the temperatures of the two sensors are the same, concentration can be replaced with relative humidity, giving

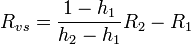
$R_{vs}=\frac{1-h_1}{h_2-h_1}R_2-R_1$

Stomatal conductance is the reciprocal of resistance, therefore

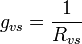$g_{vs}=\frac{1}{R_{vs}}$ .

A dynamic porometer measures how long it takes for the humidity to rise from one specified value to another in an enclosed chamber clamped to a leaf. The resistance $R$ is then determined from the following equation:

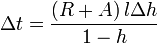
$\Delta t=\frac{\left(R+A\right)l\Delta h}{1-h}$

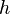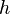where ∆ $t$ is the time required for the cup humidity to change by ∆ $h$ , $h$ is the cup humidity, 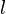$l$ is the cup “length,” and $A$ is an offset constant.

Null balance porometers maintain a constant humidity in an enclosed chamber by regulating the flow of dry air through the chamber and find stomatal resistance from the following equation:

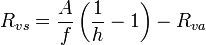
$R_{vs}=\frac{A}{f}\left(\frac{1}{h}-1\right)-R_{va}$

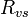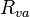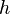where $R_{vs}$ is the stomatal resistance, $R_{va}$ is the boundary layer resistance, $A$ is the leaf area, $f$ is the flow rate of dry air, and $h$ is the chamber humidity.

The resistance values found by these equations are typically converted to conductance values.

Models

A number of models of stomatal conductance exist.

Ball-Berry-Leuning model

The Ball-Berry-Leuning model was formulated by Ball, Woodrow and Berry in 1987, and improved by Leuning in the early 90s.^[2] The model formulates stomatal conductance, $g$ as:

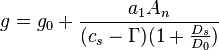
$g = g_0 + \frac{a_1 A_n}{(c_s - \Gamma) (1 + \frac{D_s}{D_0})}$

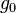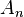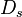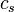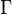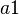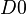Where: $g$ is the stomatal conductance for CO₂ diffusion, $g_0$ is the value of $g$ at the light compensation point, $A_n$ is CO₂ assimilation rate of the leaf, $D_s$ is the vapour pressure deficit, $c_s$ is the leaf-surface CO₂ concentration, $\Gamma$ is the CO₂ compensation point. $a1$ and $D0$ are empirical coefficients.

References

↑ Taiz/Zeiger (1991). Plant Physiology. Redwood City, CA: The Benjamin/Cummings Publishing Company, Inc. pp. 92–95. ISBN 0-8053-0245-X.
↑ Dewar, R. C. (2002). "The Ball–Berry–Leuning and Tardieu–Davies stomatal models: synthesis and extension within a spatially aggregated picture of guard cell function". Plant, Cell & Environment 25 (11): 1383–1398. doi:10.1046/j.1365-3040.2002.00909.x. ISSN 1365-3040. Retrieved 2014-12-11.