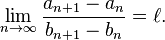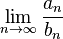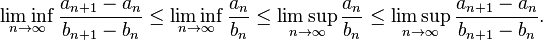Stolz–Cesàro theorem

In mathematics, the Stolz–Cesàro theorem, named after mathematicians Otto Stolz and Ernesto Cesàro, is a criterion for proving the convergence of a sequence.

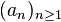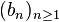Let $(a_n)_{n \geq 1}$ and $(b_n)_{n \geq 1}$ be two sequences of real numbers. Assume that 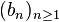$(b_n)_{n \geq 1}$ is strictly monotone and divergent sequence (i.e. strictly increasing and approaches 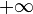$+ \infty$ or strictly decreasing and approaches 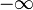$- \infty$ ) and the following limit exists:

\lim_{n \to \infty} \frac{a_{n+1}-a_n}{b_{n+1}-b_n}=\ell.\

Then, the limit

\lim_{n \to \infty} \frac{a_n}{b_n}\

also exists and it is equal to ℓ.

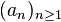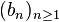The general form of the Stolz–Cesàro theorem is the following (see http://www.imomath.com/index.php?options=686): If $(a_n)_{n\geq 1}$ and $(b_n)_{n\geq 1}$ are two sequences such that 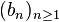$(b_n)_{n \geq 1}$ is monotone and unbounded, then:

\liminf_{n\to\infty} \frac{a_{n+1}-a_n}{b_{n+1}-b_n}\leq \liminf_{n\to\infty}\frac{a_n}{b_n}\leq\limsup_{n\to\infty}\frac{a_n}{b_n}\leq\limsup_{n\to\infty}\frac{a_{n+1}-a_n}{b_{n+1}-b_n}.

The Stolz–Cesàro theorem can be viewed as a generalization of the Cesàro mean, but also as a l'Hôpital's rule for sequences. The ∞/∞ case is stated and proved on pages 173—175 of Stolz's 1885 book S and also on page 54 of Cesàro's 1888 article C. It appears as Problem 70 in Pólya and Szegő.

References

Mureşan, Marian (2008), A Concrete Approach to Classical Analysis, Berlin: Springer, p. 85, ISBN 978-0-387-78932-3 .
Stolz, Otto (1885), Vorlesungen über allgemeine Arithmetik: nach den Neueren Ansichten, Leipzig: Teubners, pp. 173–175 .
Cesàro, Ernesto (1888), "Sur la convergence des séries", Nouvelles annales de mathématiques, Series 3 7: 49–59 .
Pólya, George; Szegő, Gábor (1925), Aufgaben und Lehrsätze aus der Analysis I, Berlin: Springer .

External links

l'Hôpital's rule and Stolz-Cesàro theorem at imomath.com

Proof of Stolz–Cesàro theorem at PlanetMath.org.

This article incorporates material from Stolz-Cesaro theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.