Stochastic processes and boundary value problems
In mathematics, some boundary value problems can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani's 1944 solution of the Dirichlet problem for the Laplace operator using Brownian motion. However, it turns out that for a large class of semi-elliptic second-order partial differential equations the associated Dirichlet boundary value problem can be solved using an Itō process that solves an associated stochastic differential equation.
Introduction: Kakutani's solution to the classical Dirichlet problem
Let D be a domain (an open and connected set) in Rn. Let Δ be the Laplace operator, let g be a bounded function on the boundary ∂D, and consider the problem
It can be shown that if a solution u exists, then u(x) is the expected value of g(x) at the (random) first exit point from D for a canonical Brownian motion starting at x. See theorem 3 in Kakutani 1944, p. 710.
The Dirichlet-Poisson problem
Let D be a domain in Rn and let L be a semi-elliptic differential operator on C2(Rn; R) of the form
where the coefficients bi and aij are continuous functions and all the eigenvalues of the matrix a(x) = (aij(x)) are non-negative. Let f ∈ C(D; R) and g ∈ C(∂D; R). Consider the Poisson problem
The idea of the stochastic method for solving this problem is as follows. First, one finds an Itō diffusion X whose infinitesimal generator A coincides with L on compactly-supported C2 functions f : Rn → R. For example, X can be taken to be the solution to the stochastic differential equation
where B is n-dimensional Brownian motion, b has components bi as above, and the matrix field σ is chosen so that
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px. Let τD denote the first exit time of X from D.
In this notation, the candidate solution for (P1) is
provided that g is a bounded function and that
It turns out that one further condition is required:
i.e., for all x, the process X starting at x almost surely leaves D in finite time. Under this assumption, the candidate solution above reduces to
and solves (P1) in the sense that if 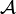 denotes the characteristic operator for X (which agrees with A on C2 functions), then
denotes the characteristic operator for X (which agrees with A on C2 functions), then
Moreover, if v ∈ C2(D; R) satisfies (P2) and there exists a constant C such that, for all x ∈ D,
then v = u.
References
- Kakutani, Shizuo (1944). "Two-dimensional Brownian motion and harmonic functions". Proc. Imp. Acad. Tokyo 20 (10): 706–714. doi:10.3792/pia/1195572706.
- Kakutani, Shizuo (1944). "On Brownian motions in n-space". Proc. Imp. Acad. Tokyo 20 (9): 648–652. doi:10.3792/pia/1195572742.
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth ed.). Berlin: Springer. ISBN 3-540-04758-1. (See Section 9)
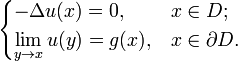
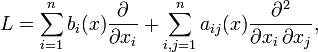
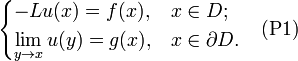
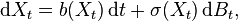
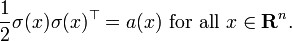
![u(x) = \mathbf{E}^{x} \left[ g \big( X_{\tau_{D}} \big) \cdot \chi_{\{ \tau_{D} < + \infty \}} \right] + \mathbf{E}^{X} \left[ \int_{0}^{\tau_{D}} f(X_{t}) \, \mathrm{d} t \right]](../I/m/cecc8b131aeda785624dc64c289f214b.png)
![\mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} \big| f(X_{t}) \big| \, \mathrm{d} t \right] < + \infty.](../I/m/62809d505903eb1ab77c391771d9adf3.png)
![\mathbf{P}^{x} \big[ \tau_{D} < + \infty \big] = 1 \mbox{ for all } x \in D,](../I/m/4292030a1499a13a6c103d6119dedfda.png)
![u(x) = \mathbf{E}^{x} \left[ g \big( X_{\tau_{D}} \big) \right] + \mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} f(X_{t}) \, \mathrm{d} t \right]](../I/m/00fbdb29ba6a6635f68620a4984a96cd.png)
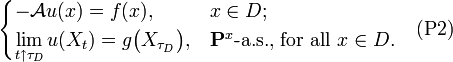
![| v(x) | \leq C \left( 1 + \mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} \big| g(X_{s}) \big| \, \mathrm{d} s \right] \right),](../I/m/78230bf339428a6c38db2f70473504e5.png)