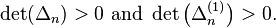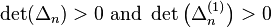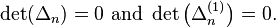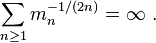Stieltjes moment problem
In mathematics, the Stieltjes moment problem, named after Thomas Joannes Stieltjes, seeks necessary and sufficient conditions for a sequence { mn, : n = 0, 1, 2, ... } to be of the form
for some measure μ. If such a function μ exists, one asks whether it is unique.
The essential difference between this and other well-known moment problems is that this is on a half-line [0, ∞), whereas in the Hausdorff moment problem one considers a bounded interval [0, 1], and in the Hamburger moment problem one considers the whole line (−∞, ∞).
Existence
Let
and
Then { mn : n = 1, 2, 3, ... } is a moment sequence of some measure on 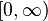 with infinite support if and only if for all n, both
with infinite support if and only if for all n, both
{ mn : n = 1, 2, 3, ... } is a moment sequence of some measure on 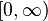 with finite support of size m if and only if for all
with finite support of size m if and only if for all 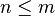 , both
, both
and for all larger 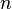
Uniqueness
There are several sufficient conditions for uniqueness, for example, Carleman's condition, which states that the solution is unique if
References
- Reed, Michael; Simon, Barry (1975), Fourier Analysis, Self-Adjointness, Methods of modern mathematical physics 2, Academic Press, p. 341 (exercise 25), ISBN 0-12-585002-6
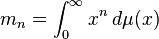
![\Delta_n=\left[\begin{matrix}
m_0 & m_1 & m_2 & \cdots & m_{n} \\
m_1 & m_2 & m_3 & \cdots & m_{n+1} \\
m_2& m_3 & m_4 & \cdots & m_{n+2} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
m_{n} & m_{n+1} & m_{n+2} & \cdots & m_{2n}
\end{matrix}\right]](../I/m/8ebdc69daad34f9fd3441d832dde0e4c.png)
![\Delta_n^{(1)}=\left[\begin{matrix}
m_1 & m_2 & m_3 & \cdots & m_{n+1} \\
m_2 & m_3 & m_4 & \cdots & m_{n+2} \\
m_3 & m_4 & m_5 & \cdots & m_{n+3} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
m_{n+1} & m_{n+2} & m_{n+3} & \cdots & m_{2n+1}
\end{matrix}\right].](../I/m/beb1f875e38634f63b523d74a3e603be.png)