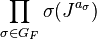Stickelberger's theorem

In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields. A special case was first proven by Ernst Kummer (1847) while the general result is due to Ludwig Stickelberger (1890).[1]

The Stickelberger element and the Stickelberger ideal

Let Km denote the mth cyclotomic field, i.e. the extension of the rational numbers obtained by adjoining the mth roots of unity to Q (where m ≥ 2 is an integer). It is a Galois extension of Q with Galois group Gm isomorphic to the multiplicative group of integers modulo m (Z/mZ)×. The Stickelberger element (of level m or of Km) is an element in the group ring Q[Gm] and the Stickelberger ideal (of level m or of Km) is an ideal in the group ring Z[Gm]. They are defined as follows. Let ζm denote a primitive mth root of unity. The isomorphism from (Z/mZ)× to Gm is given by sending a to σa defined by the relation

σa(ζm) = ζ a
m .

The Stickelberger element of level m is defined as

\theta(K_m)=\frac{1}{m}\underset{(a,m)=1}{\sum_{a=1}^m}a\cdot\sigma_a^{-1}\in\mathbf{Q}[G_m].

The Stickelberger ideal of level m, denoted I(Km), is the set of integral multiples of θ(Km) which have integral coefficients, i.e.

I(K_m)=\theta(K_m)\mathbf{Z}[G_m]\cap\mathbf{Z}[G_m].

More generally, if F be any abelian number field whose Galois group over Q is denoted GF, then the Stickelberger element of F and the Stickelberger ideal of F can be defined. By the Kronecker–Weber theorem there is an integer m such that F is contained in Km. Fix the least such m (this is the (finite part of the) conductor of F over Q). There is a natural group homomorphism Gm → GF given by restriction, i.e. if σ ∈ Gm, its image in GF is its restriction to F denoted resmσ. The Stickelberger element of F is then defined as

\theta(F)=\frac{1}{m}\underset{(a,m)=1}{\sum_{a=1}^m}a\cdot\mathrm{res}_m\sigma_a^{-1}\in\mathbf{Q}[G_F].

The Stickelberger ideal of F, denoted I(F), is defined as in the case of Km, i.e.

I(F)=\theta(F)\mathbf{Z}[G_F]\cap\mathbf{Z}[G_F].

In the special case where F = Km, the Stickelberger ideal I(Km) is generated by (a − σa)θ(Km) as a varies over Z/mZ. This not true for general F.[2]

Examples

\theta(F)=\frac{\phi(m)}{2[F:\mathbf{Q}]}\sum_{\sigma\in G_F}\sigma,
where φ is the Euler totient function and [F : Q] is the degree of F over Q.

Statement of the theorem

Stickelberger's Theorem[4]
Let F be an abelian number field. Then, the Stickelberger ideal of F annihilates the class group of F.

Note that θ(F) itself need not be an annihilator, but any multiple of it in Z[GF] is.

Explicitly, the theorem is saying that if α ∈ Z[GF] is such that

\alpha\theta(F)=\sum_{\sigma\in G_F}a_\sigma\sigma\in\mathbf{Z}[G_F]

and if J is any fractional ideal of F, then

\prod_{\sigma\in G_F}\sigma(J^{a_\sigma})

is a principal ideal.

See also

Notes

  1. ↑ Washington 1997, Notes to chapter 6
  2. ↑ Washington 1997, Lemma 6.9 and the comments following it
  3. ↑ Washington 1997, §6.2
  4. ↑ Washington 1997, Theorem 6.10

References

External links