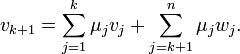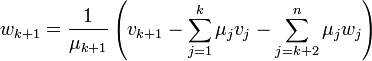Steinitz exchange lemma

The Steinitz exchange lemma is a basic theorem in linear algebra used, for example, to show that any two bases for a finite-dimensional vector space have the same number of elements. The result is named after the German mathematician Ernst Steinitz. The result is often called the Steinitz–Mac Lane exchange lemma, also recognizing the generalization[1] by Saunders Mac Lane of Steinitz's lemma to matroids.[2]

Statement

If {v1, ..., vm} is a set of m linearly independent vectors in a vector space V, and {w1, ..., wn} span V then m ≤ n and, possibly after reordering the wi, the set {v1, ..., vm, wm + 1, ..., wn} spans V.

Proof

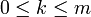We are going to show that for any integer k satisfying 0\leq k\leq m, the following assertion is valid. Choosing 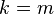k=m gives the result.

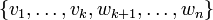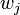(A) The set \{ v_1,\ldots, v_k,w_{k+1},\ldots,w_n\} spans V (where the w_j have possibly been reordered, and the reordering depends on k).

We will prove (A) by induction over k: Since (A) is clear for k=0, the only thing that needs to be done is the inductive step.

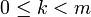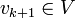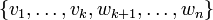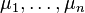Assume that (A) holds for some k satisfying 0\leq k<m. Since v_{k+1}\in V, and \{ v_1,\ldots, v_k,w_{k+1},\ldots,w_n\} spans V (by the induction hypothesis), there exist \mu_1,\ldots,\mu_n such that

v_{k+1}=\sum_{j=1}^k \mu_j v_j+\sum_{j=k+1}^n \mu_j w_j.

At least one of 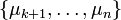\{\mu_{k+1},\ldots,\mu_n\} must be non-zero, otherwise this equality would contradict the linear independence of 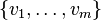\{ v_1,\ldots,v_m \}; note that this additionally implies that 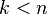k<n. By reordering the 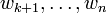w_{k+1},\ldots,w_n, we may assume that 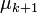\mu_{k+1} is not zero. Therefore, we have

w_{k+1}= \frac{1}{\mu_{k+1}}\left(v_{k+1} - \sum_{j=1}^k \mu_j v_j - \sum_{j=k+2}^n \mu_j w_j\right)

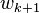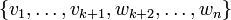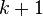In other words, w_{k+1} is in the span of \{ v_1,\ldots, v_{k+1},w_{k+2},\ldots,w_n\} and so the latter must be the whole of V. We have thus shown that (A) holds for k+1, completing the inductive step.

Applications

The Steinitz exchange lemma is a basic result in computational mathematics, especially in linear algebra and in combinatorial algorithms.[3]

References

  1. ↑ Mac Lane, Saunders (1936), "Some interpretations of abstract linear dependence in terms of projective geometry", American Journal of Mathematics (The Johns Hopkins University Press) 58 (1): 236–240, doi:10.2307/2371070, JSTOR 2371070.
  2. ↑ Kung, Joseph P. S., ed. (1986), A Source Book in Matroid Theory, Boston: Birkhäuser, ISBN 0-8176-3173-9, MR 0890330.
  3. ↑ Page v in Stiefel: Stiefel, Eduard L. (1963). An introduction to numerical mathematics (Translated by Werner C. Rheinboldt & Cornelie J. Rheinboldt from the second German ed.). New York: Academic Press. pp. x+286. MR 181077.