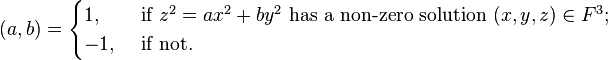Steinberg symbol

In mathematics a Steinberg symbol is a pairing function which generalises the Hilbert symbol and plays a role in the algebraic K-theory of fields. It is named after mathematician Robert Steinberg.

For a field F we define a Steinberg symbol (or simply a symbol) to be a function 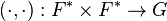$( \cdot , \cdot ) : F^* \times F^* \rightarrow G$ , where G is an abelian group, written multiplicatively, such that

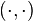$( \cdot , \cdot )$ is bimultiplicative;
if 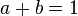$a+b = 1$ then $(a,b) = 1$ .

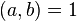The symbols on F derive from a "universal" symbol, which may be regarded as taking values in 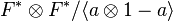$F^* \otimes F^* / \langle a \otimes 1-a \rangle$ . By a theorem of Matsumoto, this group is 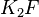$K_2 F$ and is part of the Milnor K-theory for a field.

Properties

If (⋅,⋅) is a symbol then (assuming all terms are defined)

$(a, -a) = 1$ ;
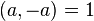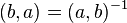$(b, a) = (a, b)^{-1}$ ;
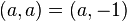$(a, a) = (a, -1)$ is an element of order 1 or 2;
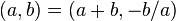$(a, b) = (a+b, -b/a)$ .

Examples

The trivial symbol which is identically 1.

The Hilbert symbol on F with values in {±1} defined by^[1]^[2]

(a,b)=\begin{cases}1,&\mbox{ if }z^2=ax^2+by^2\mbox{ has a non-zero solution }(x,y,z)\in F^3;\\-1,&\mbox{ if not.}\end{cases}

The Contou-Carrère symbol is a symbol for the ring of Laurent power series over an Artinian ring.

Continuous symbols

If F is a topological field then a symbol c is weakly continuous if for each y in F^∗ the set of x in F^∗ such that c(x,y) = 1 is closed in F^∗. This makes no reference to a topology on the codomain G. If G is a topological group, then one may speak of a continuous symbol, and when G is Hausdorff then a continuous symbol is weakly continuous.^[3]

The only weakly continuous symbols on R are the trivial symbol and the Hilbert symbol: the only weakly continuous symbol on C is the trivial symbol.^[4] The characterisation of weakly continuous symbols on a non-Archimedean local field F was obtained by Moore. The group K₂(F) is the direct sum of a cyclic group of order m and a divisible group K₂(F)^m. A symbol on F lifts to a homomorphism on K₂(F) and is weakly continuous precisely when it annihilates the divisible component K₂(F)^m. It follows that every weakly continuous symbol factors through the norm residue symbol.^[5]

References

↑ Serre, Jean-Pierre (1996). A Course in Arithmetic. Graduate Texts in Mathematics 7. Berlin, New York: Springer-Verlag. ISBN 978-3-540-90040-5.
↑ Milnor (1971) p.94
↑ Milnor (1971) p.165
↑ Milnor (1971) p.166
↑ Milnor (1971) p.175

Conner, P.E.; Perlis, R. (1984). A Survey of Trace Forms of Algebraic Number Fields. Series in Pure Mathematics 2. World Scientific. ISBN 9971-966-05-0. Zbl 0551.10017.
Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. pp. 132–142. ISBN 0-8218-1095-2. Zbl 1068.11023.
Milnor, John Willard (1971). Introduction to algebraic K-theory. Annals of Mathematics Studies 72. Princeton, NJ: Princeton University Press. MR 0349811. Zbl 0237.18005.
Steinberg, Robert (1962). "Générateurs, relations et revêtements de groupes algébriques". Colloq. Théorie des Groupes Algébriques (in French) (Bruxelles: Gauthier-Villars): 113–127. MR MR0153677. Zbl 0272.20036.

External links