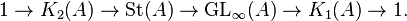Steinberg group (K-theory)
In algebraic K-theory, a field of mathematics, the Steinberg group 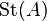 of a ring
of a ring  is the universal central extension of the commutator subgroup of the stable general linear group of
is the universal central extension of the commutator subgroup of the stable general linear group of  .
.
It is named after Robert Steinberg, and it is connected with lower  -groups, notably
-groups, notably 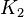 and
and 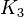 .
.
Definition
Abstractly, given a ring  , the Steinberg group
, the Steinberg group 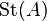 is the universal central extension of the commutator subgroup of the stable general linear group (the commutator subgroup is perfect and so has a universal central extension).
is the universal central extension of the commutator subgroup of the stable general linear group (the commutator subgroup is perfect and so has a universal central extension).
Concretely, it can be described using generators and relations.
Steinberg Relations
Elementary matrices — i.e. matrices of the form 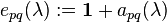 , where
, where  is the identity matrix,
is the identity matrix, 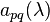 is the matrix with
is the matrix with  in the
in the  -entry and zeros elsewhere, and
-entry and zeros elsewhere, and 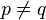 — satisfy the following relations, called the Steinberg relations:
— satisfy the following relations, called the Steinberg relations:
The unstable Steinberg group of order  over
over  , denoted by
, denoted by 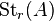 , is defined by the generators
, is defined by the generators 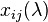 , where
, where 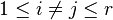 and
and 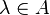 , these generators being subject to the Steinberg relations. The stable Steinberg group, denoted by
, these generators being subject to the Steinberg relations. The stable Steinberg group, denoted by 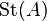 , is the direct limit of the system
, is the direct limit of the system 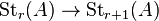 . It can also be thought of as the Steinberg group of infinite order.
. It can also be thought of as the Steinberg group of infinite order.
Mapping 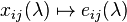 yields a group homomorphism
yields a group homomorphism 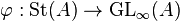 . As the elementary matrices generate the commutator subgroup, this mapping is surjective onto the commutator subgroup.
. As the elementary matrices generate the commutator subgroup, this mapping is surjective onto the commutator subgroup.
Relation to  -Theory
-Theory
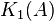 is the cokernel of the map
is the cokernel of the map 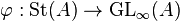 , as
, as 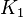 is the abelianization of
is the abelianization of 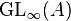 and the mapping
and the mapping 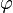 is surjective onto the commutator subgroup.
is surjective onto the commutator subgroup.
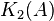 is the center of the Steinberg group. This was Milnor's definition, and it also follows from more general definitions of higher
is the center of the Steinberg group. This was Milnor's definition, and it also follows from more general definitions of higher  -groups.
-groups.
It is also the kernel of the mapping 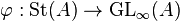 . Indeed, there is an exact sequence
. Indeed, there is an exact sequence
Equivalently, it is the Schur multiplier of the group of elementary matrices, so it is also a homology group: 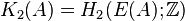 .
.
Gersten (1973) showed that 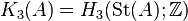 .
.
References
- Gersten, S. M. (1973), "
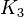 of a Ring is
of a Ring is 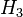 of the Steinberg Group", Proceedings of the American Mathematical Society (American Mathematical Society) 37 (2): 366–368, doi:10.2307/2039440, JSTOR 2039440
of the Steinberg Group", Proceedings of the American Mathematical Society (American Mathematical Society) 37 (2): 366–368, doi:10.2307/2039440, JSTOR 2039440
- Milnor, John Willard (1971), Introduction to Algebraic
 -theory, Annals of Mathematics Studies 72, Princeton University Press, MR 0349811
-theory, Annals of Mathematics Studies 72, Princeton University Press, MR 0349811
- Steinberg, Robert (1968), Lectures on Chevalley Groups, Yale University, New Haven, Conn., MR 0466335
![\begin{align}
e_{ij}(\lambda) e_{ij}(\mu) & = e_{ij}(\lambda+\mu); && \\
\left[ e_{ij}(\lambda),e_{jk}(\mu) \right] & = e_{ik}(\lambda \mu), && \text{for } i \neq k; \\
\left[ e_{ij}(\lambda),e_{kl}(\mu) \right] & = \mathbf{1}, && \text{for } i \neq l \text{ and } j \neq k.
\end{align}](../I/m/87e018ab1e84a8e3117f835983cc02db.png)