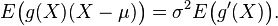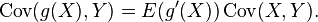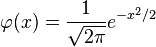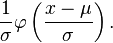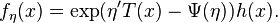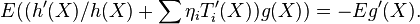Stein's lemma

Stein's lemma,^[1] named in honor of Charles Stein, is a theorem of probability theory that is of interest primarily because of its applications to statistical inference — in particular, to James–Stein estimation and empirical Bayes methods — and its applications to portfolio choice theory.

Statement of the lemma

Suppose X is a normally distributed random variable with expectation μ and variance σ². Further suppose g is a function for which the two expectations E(g(X) (X − μ) ) and E( g ′(X) ) both exist (the existence of the expectation of any random variable is equivalent to the finiteness of the expectation of its absolute value). Then

E\bigl(g(X)(X-\mu)\bigr)=\sigma^2 E\bigl(g'(X)\bigr).

In general, suppose X and Y are jointly normally distributed. Then

\operatorname{Cov}(g(X),Y)=E(g'(X)) \operatorname{Cov}(X,Y).

In order to prove the univariate version of this lemma, recall that the probability density function for the normal distribution with expectation 0 and variance 1 is

\varphi(x)={1 \over \sqrt{2\pi}}e^{-x^2/2}

and that for a normal distribution with expectation μ and variance σ² is

{1\over\sigma}\varphi\left({x-\mu \over \sigma}\right).

Then use integration by parts.

More general statement

Suppose X is in an exponential family, that is, X has the density

f_\eta(x)=\exp(\eta'T(x) - \Psi(\eta))h(x).

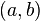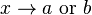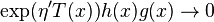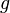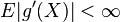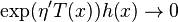Suppose this density has support $(a,b)$ where $a,b$ could be $-\infty ,\infty$ and as $x\rightarrow a\text{ or }b$ , $\exp (\eta'T(x))h(x) g(x) \rightarrow 0$ where $g$ is any differentiable function such that $E|g'(X)|<\infty$ or $\exp (\eta'T(x))h(x) \rightarrow 0$ if $a,b$ finite. Then

E((h'(X)/h(X) + \sum \eta_i T_i'(X))g(X)) = -Eg'(X).

The derivation is same as the special case, namely, integration by parts.

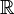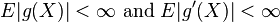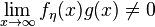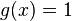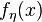If we only know $X$ has support $\mathbb{R}$ , then it could be the case that $E|g(X)| <\infty \text{ and } E|g'(X)| <\infty$ but $\lim_{x\rightarrow \infty} f_\eta(x) g(x) \not= 0$ . To see this, simply put $g(x)=1$ and $f_\eta(x)$ with infinitely spikes towards infinity but still integrable. One such example could be adapted from 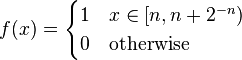$f(x) = \begin{cases} 1 & x \in [n, n + 2^{-n}) \\ 0 & \text{otherwise} \end{cases}$ so that $f$ is smooth.

Extensions to elliptically-contoured distributions also exist.^[2]^[3]

References

↑ Ingersoll, J., Theory of Financial Decision Making, Rowman and Littlefield, 1987: 13-14.
↑ Hamada, Mahmoud; Valdez, Emiliano A. (2008). "CAPM and option pricing with elliptically contoured distributions". The Journal of Risk & Insurance 75 (2): 387–409. doi:10.1111/j.1539-6975.2008.00265.x.
↑ Landsman, Zinoviy; Nešlehová, Johanna (2008). "Stein's Lemma for elliptical random vectors". Journal of Multivariate Analysis 99 (5): 912––927. doi:10.1016/j.jmva.2007.05.006.