Statistical coupling analysis
Statistical coupling analysis or SCA is a technique used in bioinformatics to measure covariation between pairs of amino acids in a protein multiple sequence alignment (MSA). More specifically, it quantifies how much the amino acid distribution at some position i changes upon a perturbation of the amino acid distribution at another position j. The resulting statistical coupling energy indicates the degree of evolutionary dependence between the residues, with higher coupling energy corresponding to increased dependence.[1]
Definition of statistical coupling energy
Statistical coupling energy measures how a perturbation of amino acid distribution at one site in an MSA affects the amino acid distribution at another site. For example, consider a multiple sequence alignment with sites (or columns) a through z, where each site has some distribution of amino acids. At position i, 60% of the sequences have a valine and the remaining 40% of sequences have a leucine, at position j the distribution is 40% isoleucine, 40% histidine and 20% methionine, k has an average distribution (the 20 amino acids are present at roughly the same frequencies seen in all proteins), and l has 80% histidine, 20% valine. Since positions i, j and l have an amino acid distribution different from the mean distribution observed in all proteins, they are said to have some degree of conservation.
In statistical coupling analysis, the conservation (ΔGstat) at each site (i) is defined as: 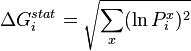 .[2]
.[2]
Here, Pix describes the probability of finding amino acid x at position i, and is defined by a function in binomial form as follows:
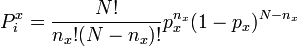 ,
,where N is 100, nx is the percentage of sequences with residue x (e.g. methionine) at position i, and px corresponds to the approximate distribution of amino acid x in all positions among all sequenced proteins. The summation runs over all 20 amino acids. After ΔGistat is computed, the conservation for position i in a subalignment produced after a perturbation of amino acid distribution at j (ΔGi | δjstat) is taken. Statistical coupling energy, denoted ΔΔGi, jstat, is simply the difference between these two values. That is:
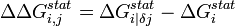 , or, more commonly,
, or, more commonly, 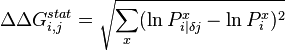
Statistical coupling energy is often systematically calculated between a fixed, perturbated position, and all other positions in an MSA. Continuing with the example MSA from the beginning of the section, consider a perturbation at position j where the amino distribution changes from 40% I, 40% H, 20% M to 100% I. If, in a subsequent subalignment, this changes the distribution at i from 60% V, 40% L to 90% V, 10% L, but does not change the distribution at position l, then there would be some amount of statistical coupling energy between i and j but none between l and j.
Applications
Ranganathan and Lockless originally developed SCA to examine thermodynamic (energetic) coupling of residue pairs in proteins.[3] Using the PDZ domain family, they were able to identify a small network of residues that were energetically coupled to a binding site residue. The network consisted of both residues spatially close to the binding site in the tertiary fold, called contact pairs, and more distant residues that participate in longer-range energetic interactions. Later applications of SCA by the Ranganathan group on the GPCR, serine protease and hemoglobin families also showed energetic coupling in sparse networks of residues that cooperate in allosteric communication.[4]
Statistical coupling analysis has also been used as a basis for computational protein design. In 2005, Russ et al.[5] used an SCA for the WW domain to create artificial proteins with similar thermodynamic stability and structure to natural WW domains. The fact that 12 out of the 43 designed proteins with the same SCA profile as natural WW domains properly folded provided strong evidence that little information—only coupling information—was required for specifying the protein fold. This support for the SCA hypothesis was made more compelling considering that a) the successfully folded proteins had only 36% average sequence identity to natural WW folds, and b) none of the artificial proteins designed without coupling information folded properly. An accompanying study showed that the artificial WW domains were functionally similar to natural WW domains in ligand binding affinity and specificity.[6]
In de novo protein structure prediction, it has been shown that, when combined with a simple residue-residue distance metric, SCA-based scoring can fairly accurately distinguish native from non-native protein folds.[7]
See also
External links
- What is a WW domain?
- Ranganathan lecture on statistical coupling analysis (audio included)
- Protein folding — a step closer? - A summary of the Ranganathan lab's SCA-based design of artificial yet functional WW domains.
References
- ↑ "Supplementary Material for 'Evolutionarily conserved networks of residues mediate allosteric communication in proteins.'".
- ↑ Dekker; Fodor, A; Aldrich, RW; Yellen, G et al. (2004). "A perturbation-based method for calculating explicit likelihood of evolutionary co-variance in multiple sequence alignments". Bioinformatics 20 (10): 1565–1572. doi:10.1093/bioinformatics/bth128. PMID 14962924.
- ↑ Lockless SW, Ranaganathan R (1999). "Evolutionarily conserved pathways of energetic connectivity in protein families". Science 286 (5438): 295–299. doi:10.1126/science.286.5438.295. PMID 10514373.
- ↑ Suel; Lockless, SW; Wall, MA; Ranganathan, R et al. (2003). "Evolutionarily conserved networks of residues mediate allosteric communication in proteins.". Nature Structural Biology 10 (1): 59–69. doi:10.1038/nsb881. PMID 12483203.
- ↑ Socolich; Lockless, SW; Russ, WP; Lee, H; Gardner, KH; Ranganathan, R et al. (2005). "Evolutionary information for specifying a protein fold". Nature 437 (7058): 512–518. doi:10.1038/nature03991. PMID 16177782.
- ↑ Russ; Lowery, DM; Mishra, P; Yaffe, MB; Ranganathan, R et al. (2005). "Natural-like function in artificial WW domains". Nature 437 (7058): 579–583. doi:10.1038/nature03990. PMID 16177795.
- ↑ Bartlett GJ, Taylor WR (2008). "Using scores derived from statistical coupling analysis to distinguish correct and incorrect folds in de-novo protein structure prediction.". Proteins 71 (1): 950–959. doi:10.1002/prot.21779. PMID 18004776.