State prices
In financial economics, a state-price security, also called an Arrow-Debreu security (from its origins in the Arrow-Debreu model), a pure security, or a primitive security is a contract that agrees to pay one unit of a numeraire (a currency or a commodity) if a particular state occurs at a particular time in the future and pays zero numeraire in all the other states. The price of this security is the state price of this particular state of the world, which may be represented by a vector. The state price vector is the vector of state prices for all states.[1][2][3]
As such, any derivatives contract whose settlement value is a function of an underlying whose value is uncertain at contract date can be decomposed as a linear combination of its Arrow-Debreu securities, and thus as a weighted sum of its state prices.
The Arrow-Debreu model (also referred to as the Arrow-Debreu-McKenzie model or ADM model) is the central model in the General Equilibrium Theory and uses state prices in the process of proving the existence of a unique general equilibrium.
Example
Imagine a world where two states are possible tomorrow: peace (P) and war (W). Denote the random variable which represents the state as ω; denote tomorrow's random variable as ω1. Thus, ω1 can take two values: ω1=P and ω1=W.
Let's imagine that:
- There is a security that pays off £1 if tomorrow's state is "P" and nothing if the state is "W". The price of this security is qP
- There is a security that pays off £1 if tomorrow's state is "W" and nothing if the state is "P". The price of this security is qW
The prices qP and qW are the state prices.
The factors that affect these state prices are:
- The probabilities of ω1=P and ω1=W. The more likely a move to W is, the higher the price qW gets, since qW insures the agent against the occurrence of state W. The seller of this insurance would demand a higher premium (if the economy is efficient).
- The preferences of the agent. Suppose the agent has a standard concave utility function which depends on the state of the world. Assume that the agent loses an equal amount if the state is "W" as he would gain if the state was "P". Now, even if you assume that the above-mentioned probabilities ω1=P and ω1=W are equal, the changes in utility for the agent are not: Due to his decreasing marginal utility, the utility gain from a "peace dividend" tomorrow would be lower than the utility lost from the "war" state. If our agent were rational, he would pay more to insure against the down state than his net gain from the up state would be.
Application to financial assets
If the agent buys both qP and qW, he has secured £1 for tomorrow. He has purchased a riskless bond. The price of the bond is b0 = qP + qW.
Now consider a security with state-dependent payouts (e.g. an equity security, an option, a risky bond etc.). It pays ck if ω1=k -- i.e. it pays cP in peacetime and cW in wartime). The price of this security is c0 = qPcP + qWcW.
Generally, the usefulness of state prices arises from their linearity: Any security can be valued as the sum over all possible states of state price times payoff in that state: 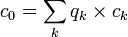 .
.
Analogously, for a continuous random variable indicating a continuum of possible states, the value is found by integrating over the state price density.
See also
References
- ↑ economics.about.com Accessed June 18, 2008
- ↑ Rebonato, R. (2005). Volatility and correlation: the perfect hedger and the fox. John Wiley & Sons. http://books.google.co.uk/books?id=HD9P6L2zX48C&pg=PA323&dq=arrow+debreu+state+price&hl=en&sa=X&ei=U2xwVJjAA9P3aqWJgMAH&redir_esc=y#v=onepage&q=arrow%20debreu%20state%20price&f=false
- ↑ Dupire, B. (1997). Pricing and hedging with smiles (pp. 103-112). in: Mathematics of derivative securities. Dempster and Pliska eds., Cambridge Uni. Press.