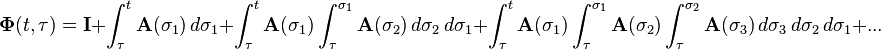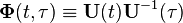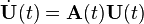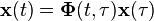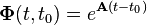State-transition matrix

In control theory, the state-transition matrix is a matrix whose product with the state vector $x$ at an initial time $t_0$ gives $x$ at a later time $t$ . The state-transition matrix can be used to obtain the general solution of linear dynamical systems.

Linear systems solutions

The state-transition matrix is used to find the solution to a general state-space representation of a linear system in the following form

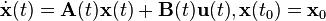\dot{\mathbf{x}}(t) = \mathbf{A}(t) \mathbf{x}(t) + \mathbf{B}(t) \mathbf{u}(t) , \mathbf{x}(t_0) = \mathbf{x}_0

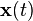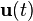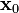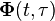where $\mathbf{x}(t)$ are the states of the system, $\mathbf{u}(t)$ is the input signal, and $\mathbf{x}_0$ is the initial condition at $t_0$ . Using the state-transition matrix $\mathbf{\Phi}(t, \tau)$ , the solution is given by:^[1]^[2]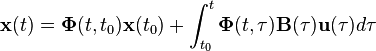 $\mathbf{x}(t)= \mathbf{\Phi} (t, t_0)\mathbf{x}(t_0)+\int_{t_0}^t \mathbf{\Phi}(t, \tau)\mathbf{B}(\tau)\mathbf{u}(\tau)d\tau$

Peano-Baker series

The most general transition matrix is given by the Peano-Baker series

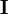\mathbf{\Phi}(t,\tau) = \mathbf{I} + \int_\tau^t\mathbf{A}(\sigma_1)\,d\sigma_1 + \int_\tau^t\mathbf{A}(\sigma_1)\int_\tau^{\sigma_1}\mathbf{A}(\sigma_2)\,d\sigma_2\,d\sigma_1 + \int_\tau^t\mathbf{A}(\sigma_1)\int_\tau^{\sigma_1}\mathbf{A}(\sigma_2)\int_\tau^{\sigma_2}\mathbf{A}(\sigma_3)\,d\sigma_3\,d\sigma_2\,d\sigma_1 + ...

where $\mathbf{I}$ is the identity matrix. This matrix converges uniformly and absolutely to a solution that exists and is unique.^[2]

Other properties

The state-transition matrix 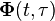$\mathbf{\Phi}(t, \tau)$ , given by

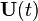\mathbf{\Phi}(t, \tau)\equiv\mathbf{U}(t)\mathbf{U}^{-1}(\tau)

where $\mathbf{U}(t)$ is the fundamental solution matrix that satisfies

\dot{\mathbf{U}}(t)=\mathbf{A}(t)\mathbf{U}(t)

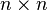is a $n \times n$ matrix that is a linear mapping onto itself, i.e., with 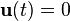$\mathbf{u}(t)=0$ , given the state $\mathbf{x}(\tau)$ at any time $\tau$ , the state at any other time $t$ is given by the mapping

\mathbf{x}(t)=\mathbf{\Phi}(t, \tau)\mathbf{x}(\tau)

The state transition matrix must always satisfy the following relationships:

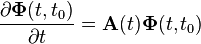\frac{\partial \mathbf{\Phi}(t, t_0)}{\partial t} = \mathbf{A}(t)\mathbf{\Phi}(t, t_0)

and

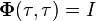\mathbf{\Phi}(\tau, \tau) = I

for all

\tau

and where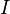

I

is the identity matrix.^[3]

And 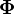$\mathbf{\Phi}$ ; also must have the following properties:

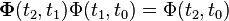
1.	$\mathbf{\Phi}(t_2, t_1)\Phi(t_1, t_0) = \Phi(t_2, t_0)$
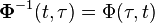
2.	$\mathbf{\Phi}^{-1}(t, \tau) = \Phi(\tau, t)$
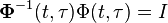
3.	$\mathbf{\Phi}^{-1}(t, \tau)\Phi(t, \tau) = I$
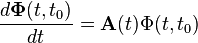
4.	$\frac{d\mathbf{\Phi}(t, t_0)}{dt} = \mathbf{A}(t)\Phi(t, t_0)$

If the system is time-invariant, we can define 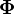$\mathbf{\Phi}$ ; as:

\mathbf{\Phi}(t, t_0) = e^{\mathbf{A}(t - t_0)}

In the time-variant case, there are many different functions that may satisfy these requirements, and the solution is dependent on the structure of the system. The state-transition matrix must be determined before analysis on the time-varying solution can continue.

Notes

Baake, M.; Schlaegel, U. (2011). "The Peano Baker Series". Proceedings of the Steklov Institute of Mathematics 275. pp. 155–159.
Brogan, W.L. (1991). Modern Control Theory. Prentice Hall. ISBN 0-13-589763-7.

References

↑ Baake, Michael; Schlaegel, Ulrike (2011). "The Peano Baker Series". Proceeding of the Steklov Institute of Mathematics 275: 155–159.
↑ 2.0 2.1 Rugh, Wilson (1996). Linear System Theory. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-441205-2.
↑ Brockett, Roger W. (1970). Finite Dimensional Linear Systems. John Wiley & Sons. ISBN 978-0-471-10585-5.

Wikibooks has a book on the topic of: Control Systems/Time Variant System Solutions