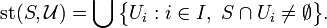Star refinement
In mathematics, specifically in the study of topology and open covers of a topological space X, a star refinement is a particular kind of refinement of an open cover of X.
The general definition makes sense for arbitrary coverings and does not require a topology. Let  be a set and let
be a set and let 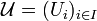 be a covering of
be a covering of  , i.e.,
, i.e., 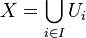 . Given a subset
. Given a subset  of
of  then the star of
then the star of  with respect to
with respect to 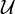 is the union of all the sets
is the union of all the sets 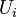 that intersect
that intersect  , i.e.:
, i.e.:
Given a point 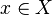 , we write
, we write 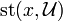 instead of
instead of 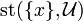 .
.
The covering 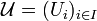 of
of  is said to be a refinement of a covering
is said to be a refinement of a covering 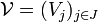 of
of  if every
if every 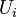 is contained in some
is contained in some 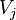 . The covering
. The covering 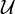 is said to be a barycentric refinement of
is said to be a barycentric refinement of 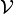 if for every
if for every 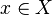 the star
the star 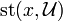 is contained in some
is contained in some 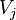 . Finally, the covering
. Finally, the covering 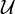 is said to be a star refinement of
is said to be a star refinement of 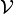 if for every
if for every 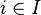 the star
the star 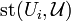 is contained in some
is contained in some 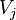 .
.
Star refinements are used in the definition of fully normal space and in one definition of uniform space. It is also useful for stating a characterization of paracompactness.
References
- J. Dugundji, Topology, Allyn and Bacon Inc., 1966.
- Lynn Arthur Steen and J. Arthur Seebach, Jr.; 1970; Counterexamples in Topology; 2nd (1995) Dover edition ISBN 0-486-68735-X; page 165.