Star-free language
A regular language is said to be star-free if it can be described by a regular expression constructed from the letters of the alphabet, the empty set symbol, all boolean operators – including complementation – and concatenation but no Kleene star.[1] For instance, the language of words over the alphabet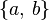 
that do not have consecutive a's can be defined by 
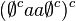, where 
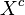denotes the complement of a subset 
of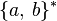 
. The condition is equivalent to having generalized star height zero.
Marcel-Paul Schützenberger characterized star-free languages as those with aperiodic syntactic monoids.[2][3] They can also be characterized logically as languages definable in FO[<], the monadic first-order logic over the natural numbers with the less-than relation,[4] as the counter-free languages[5] and as languages definable in linear temporal logic.[6]
All star-free languages are in uniform AC0.
See also
References
- ↑ Lawson (2004) p.235
- ↑ Marcel-Paul Schützenberger (1965). "On finite monoids having only trivial subgroups" (PDF). Information and Computation 8 (2): 190–194. doi:10.1016/s0019-9958(65)90108-7.
- ↑ Lawson (2004) p.262
- ↑ Straubing, Howard (1994). Finite automata, formal logic, and circuit complexity. Progress in Theoretical Computer Science. Basel: Birkhäuser. p. 79. ISBN 3-7643-3719-2. Zbl 0816.68086.
- ↑ McNaughton, Robert; Papert, Seymour (1971). Counter-free Automata. Research Monograph 65. With an appendix by William Henneman. MIT Press. ISBN 0-262-13076-9. Zbl 0232.94024.
- ↑ Kamp, Johan Antony Willem (1968). Tense Logic and the Theory of Linear Order. University of California at Los Angeles (UCLA).
- Lawson, Mark V. (2004). Finite automata. Chapman and Hall/CRC. ISBN 1-58488-255-7. Zbl 1086.68074.
- Diekert, Volker; Gastin, Paul (2008). "First-order definable languages". In Jörg Flum; Erich Grädel; Thomas Wilke. Logic and automata: history and perspectives (PDF). Amsterdam University Press. ISBN 978-90-5356-576-6.
| |||||||||||||||||||