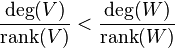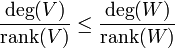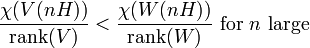Stable vector bundle

In mathematics, a stable vector bundle is a vector bundle that is stable in the sense of geometric invariant theory. They were defined by Mumford (1963).

Stable vector bundles over curves

A bundle W over an algebraic curve (or over a Riemann surface) is stable if and only if

\displaystyle\frac{\deg(V)}{\hbox{rank}(V)} < \frac{\deg(W)}{\hbox{rank}(W)}

for all proper non-zero subbundles V of W and is semistable if

\displaystyle\frac{\deg(V)}{\hbox{rank}(V)} \le \frac{\deg(W)}{\hbox{rank}(W)}

for all proper non-zero subbundles V of W. Informally this says that a bundle is stable if it is "more ample" than any proper subbundle, and is unstable if it contains a "more ample" subbundle. The moduli space of stable bundles of given rank and degree is an algebraic variety.

Narasimhan & Seshadri (1965) showed that stable bundles on projective nonsingular curves are the same as those that have projectively flat unitary irreducible connections; these correspond to irreducible unitary representations of the fundamental group. Kobayashi and Hitchin conjectured an analogue of this in higher dimensions; this was proved for projective nonsingular surfaces by Donaldson (1985), who showed that in this case a vector bundle is stable if and only if it has an irreducible Hermitian–Einstein connection.

The cohomology of the moduli space of stable vector bundles over a curve was described by Harder & Narasimhan (1975) and Atiyah & Bott (1983).

Stable vector bundles over projective varieties

If X is a smooth projective variety of dimension n and H is a hyperplane section, then a vector bundle (or torsionfree sheaf) W is called stable if

\frac{\chi(V(nH))}{\hbox{rank}(V)} < \frac{\chi(W(nH))}{\hbox{rank}(W)}\text{ for }n\text{ large}

for all proper non-zero subbundles (or subsheaves) V of W, where 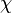$\chi$ denotes the Euler characteristic of an algebraic vector bundle and the vector bundle 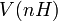$V(nH)$ means the n-th twist of V by H. W is called semistable if the above holds with < replaced by ≤.

There are also other variants in the literature: cf. this thesis p.29.

References

Atiyah, Michael Francis; Bott, Raoul (1983), "The Yang-Mills equations over Riemann surfaces", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 308 (1505): 523–615, doi:10.1098/rsta.1983.0017, ISSN 0080-4614, JSTOR 37156, MR 702806
Donaldson, S. K. (1985), "Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles", Proceedings of the London Mathematical Society. Third Series 50 (1): 1–26, doi:10.1112/plms/s3-50.1.1, ISSN 0024-6115, MR 765366
Friedman, Robert (1998), Algebraic surfaces and holomorphic vector bundles, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98361-5, MR 1600388
Harder, G.; Narasimhan, M. S. (1975), "On the cohomology groups of moduli spaces of vector bundles on curves", Mathematische Annalen 212 (3): 215–248, doi:10.1007/BF01357141, ISSN 0025-5831, MR 0364254
Mumford, David (1963), "Projective invariants of projective structures and applications", Proc. Internat. Congr. Mathematicians (Stockholm, 1962), Djursholm: Inst. Mittag-Leffler, pp. 526–530, MR 0175899
Mumford, David; Fogarty, J.; Kirwan, F. (1994), Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)] 34 (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56963-3, MR 1304906 especially appendix 5C.
Narasimhan, M. S.; Seshadri, C. S. (1965), "Stable and unitary vector bundles on a compact Riemann surface", Annals of Mathematics. Second Series (The Annals of Mathematics, Vol. 82, No. 3) 82 (3): 540–567, doi:10.2307/1970710, ISSN 0003-486X, JSTOR 1970710, MR 0184252

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves

Stable vector bundle

Stable vector bundles over curves

Stable vector bundles over projective varieties

See also

References