Stabilizer code
The theory of quantum error correction plays a prominent role in the practical realization and engineering of quantum computing and quantum communication devices. The first quantum error-correcting codes are strikingly similar to classical block codes in their operation and performance. Quantum error-correcting codes restore a noisy, decohered quantum state to a pure quantum state. A stabilizer quantum error-correcting code appends ancilla qubits to qubits that we want to protect. A unitary encoding circuit rotates the global state into a subspace of a larger Hilbert space. This highly entangled, encoded state corrects for local noisy errors. A quantum error-correcting code makes quantum computation and quantum communication practical by providing a way for a sender and receiver to simulate a noiseless qubit channel given a noisy qubit channel that has a particular error model.
The stabilizer theory of quantum error correction allows one to import some classical binary or quaternary codes for use as a quantum code. The only "catch" when importing is that the classical code must satisfy the dual-containing or self-orthogonality constraint. Researchers have found many examples of classical codes satisfying this constraint, but most classical codes do not. Nevertheless, it is still useful to import classical codes in this way (though, see how the entanglement-assisted stabilizer formalism overcomes this difficulty).
Mathematical background
The Stabilizer formalism exploits elements of
the Pauli group 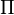 in formulating quantum error-correcting codes. The set
in formulating quantum error-correcting codes. The set
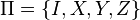 consists of the Pauli operators:
consists of the Pauli operators:
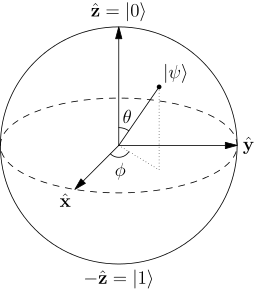
The above operators act on a single qubit---a state represented by a vector in a two-dimensional
Hilbert space. Operators in 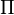 have eigenvalues
have eigenvalues 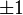 and either commute
or anti-commute. The set
and either commute
or anti-commute. The set 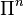 consists of
consists of  -fold tensor products of
Pauli operators:
-fold tensor products of
Pauli operators:
Elements of 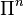 act on a quantum register of
act on a quantum register of  qubits. We
occasionally omit tensor product symbols in what follows so that
qubits. We
occasionally omit tensor product symbols in what follows so that
The  -fold Pauli group
-fold Pauli group
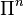 plays an important role for both the encoding circuit and the
error-correction procedure of a quantum stabilizer code over
plays an important role for both the encoding circuit and the
error-correction procedure of a quantum stabilizer code over  qubits.
qubits.
Definition
Let us define an ![\left[ n,k\right]](../I/m/2db1bd59f8f6e8ce81c7101f5ee5bbe5.png) stabilizer quantum error-correcting
code to encode
stabilizer quantum error-correcting
code to encode  logical qubits into
logical qubits into  physical qubits. The rate of such a
code is
physical qubits. The rate of such a
code is 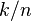 . Its stabilizer
. Its stabilizer  is an abelian subgroup of the
is an abelian subgroup of the
 -fold Pauli group
-fold Pauli group 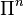 :
: 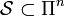 .
.  does not contain the operator
does not contain the operator 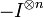 . The simultaneous
. The simultaneous
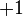 -eigenspace of the operators constitutes the codespace. The
codespace has dimension
-eigenspace of the operators constitutes the codespace. The
codespace has dimension 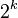 so that we can encode
so that we can encode  qubits into it. The
stabilizer
qubits into it. The
stabilizer  has a minimal representation in terms of
has a minimal representation in terms of 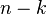 independent generators
independent generators
The generators are
independent in the sense that none of them is a product of any other two (up
to a global phase). The operators 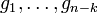 function in the same
way as a parity check matrix does for a classical linear block code.
function in the same
way as a parity check matrix does for a classical linear block code.
Stabilizer error-correction conditions
One of the fundamental notions in quantum error correction theory is that it
suffices to correct a discrete error set with support in the Pauli group
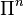 . Suppose that the errors affecting an
encoded quantum state are a subset
. Suppose that the errors affecting an
encoded quantum state are a subset 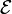 of the Pauli group
of the Pauli group 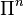 :
:
An error 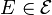 that affects an
encoded quantum state either commutes or anticommutes with any particular
element
that affects an
encoded quantum state either commutes or anticommutes with any particular
element  in
in  . The error
. The error  is correctable if it
anticommutes with an element
is correctable if it
anticommutes with an element  in
in  . An anticommuting error
. An anticommuting error
 is detectable by measuring each element
is detectable by measuring each element  in
in  and
computing a syndrome
and
computing a syndrome 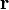 identifying
identifying  . The syndrome is a binary
vector
. The syndrome is a binary
vector 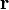 with length
with length 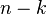 whose elements identify whether the
error
whose elements identify whether the
error  commutes or anticommutes with each
commutes or anticommutes with each 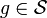 . An error
. An error
 that commutes with every element
that commutes with every element  in
in  is correctable if
and only if it is in
is correctable if
and only if it is in  . It corrupts the encoded state if it
commutes with every element of
. It corrupts the encoded state if it
commutes with every element of  but does not lie in
but does not lie in 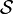 . So we compactly summarize the stabilizer error-correcting conditions: a
stabilizer code can correct any errors
. So we compactly summarize the stabilizer error-correcting conditions: a
stabilizer code can correct any errors 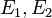 in
in 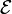 if
if
or
where 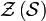 is the centralizer of
is the centralizer of  .
.
Relation between Pauli group and binary vectors
A simple but useful mapping exists between elements of 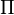 and the binary
vector space
and the binary
vector space 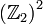 . This mapping gives a
simplification of quantum error correction theory. It represents quantum codes
with binary vectors and binary operations rather than with Pauli operators and
matrix operations respectively.
. This mapping gives a
simplification of quantum error correction theory. It represents quantum codes
with binary vectors and binary operations rather than with Pauli operators and
matrix operations respectively.
We first give the mapping for the one-qubit case. Suppose ![\left[ A\right]](../I/m/b85521eb6c1b3d94bc8af1ebced2e36a.png) is a set of equivalence classes of an operator
is a set of equivalence classes of an operator  that have the same phase:
that have the same phase:
Let ![\left[ \Pi\right]](../I/m/1c628122caada9b0604657a28ec67345.png) be the set of phase-free Pauli operators where
be the set of phase-free Pauli operators where
![\left[ \Pi\right] =\left\{ \left[ A\right] \ |\ A\in\Pi\right\}](../I/m/e88da6d1ed983546a8178bfd1bb2179a.png) .
Define the map
.
Define the map 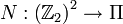 as
as
Suppose 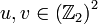 . Let us employ the
shorthand
. Let us employ the
shorthand 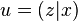 and
and 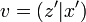 where
where 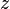 ,
,  ,
, 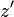 ,
, 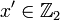 . For
example, suppose
. For
example, suppose 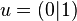 . Then
. Then 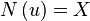 . The
map
. The
map  induces an isomorphism
induces an isomorphism ![\left[ N\right] :\left( \mathbb{Z}
_{2}\right) ^{2}\rightarrow\left[ \Pi\right]](../I/m/bf6e420010746954084a3e458c00156f.png) because addition of vectors
in
because addition of vectors
in 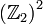 is equivalent to multiplication of
Pauli operators up to a global phase:
is equivalent to multiplication of
Pauli operators up to a global phase:
Let 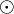 denote the symplectic product between two elements
denote the symplectic product between two elements 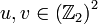 :
:
The symplectic product 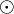 gives the commutation relations of elements of
gives the commutation relations of elements of
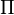 :
:
The symplectic product and the mapping  thus give a useful way to phrase
Pauli relations in terms of binary algebra.
The extension of the above definitions and mapping
thus give a useful way to phrase
Pauli relations in terms of binary algebra.
The extension of the above definitions and mapping  to multiple qubits is
straightforward. Let
to multiple qubits is
straightforward. Let 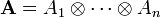 denote an
arbitrary element of
denote an
arbitrary element of 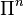 . We can similarly define the phase-free
. We can similarly define the phase-free
 -qubit Pauli group
-qubit Pauli group ![\left[ \Pi^{n}\right] =\left\{ \left[
\mathbf{A}\right] \ |\ \mathbf{A}\in\Pi^{n}\right\}](../I/m/fdc34c668a5b5aaeb99df053d5bbf930.png) where
where
The group operation 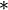 for the above equivalence class is as follows:
for the above equivalence class is as follows:
The equivalence class ![\left[ \Pi^{n}\right]](../I/m/89158eb0f17642ef2bd9dbac63912d5f.png) forms a commutative group
under operation
forms a commutative group
under operation 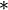 . Consider the
. Consider the 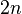 -dimensional vector space
-dimensional vector space
It forms the commutative group 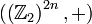 with
operation
with
operation 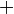 defined as binary vector addition. We employ the notation
defined as binary vector addition. We employ the notation
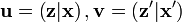 to represent any vectors
to represent any vectors
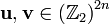 respectively. Each
vector
respectively. Each
vector  and
and 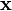 has elements
has elements 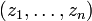 and
and 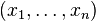 respectively with
similar representations for
respectively with
similar representations for 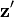 and
and 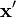 .
The symplectic product
.
The symplectic product 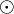 of
of 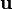 and
and 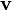 is
is
or
where 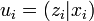 and
and 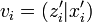 . Let us define a map
. Let us define a map 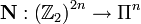 as follows:
as follows:
Let
so that 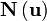 and
and 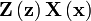 belong to the same
equivalence class:
belong to the same
equivalence class:
The map ![\left[ \mathbf{N}\right] :\left( \mathbb{Z}_{2}\right)
^{2n}\rightarrow\left[ \Pi^{n}\right]](../I/m/4ddd77e5d930b2cefc598ea448c308fb.png) is an isomorphism for the same
reason given as the previous case:
is an isomorphism for the same
reason given as the previous case:
where 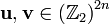 . The symplectic product
captures the commutation relations of any operators
. The symplectic product
captures the commutation relations of any operators 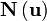 and
and 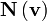 :
:
The above binary representation and symplectic algebra are useful in making the relation between classical linear error correction and quantum error correction more explicit.
By comparing quantum error correcting codes in this language to symplectic vector spaces, we can see the following. A symplectic subspace corresponds to a direct sum of Pauli algebras (i.e., encoded qubits), while an isotropic subspace corresponds to a set of stabilizers.
Example of a stabilizer code
An example of a stabilizer code is the five qubit
![\left[ 5,1\right]](../I/m/058bf6eb0e43a1d88d017a1744ce6e95.png) stabilizer code. It encodes
stabilizer code. It encodes 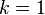 logical qubit
into
logical qubit
into 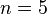 physical qubits and protects against an arbitrary single-qubit
error. Its stabilizer consists of
physical qubits and protects against an arbitrary single-qubit
error. Its stabilizer consists of 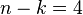 Pauli operators:
Pauli operators:
The above operators commute. Therefore the codespace is the simultaneous
+1-eigenspace of the above operators. Suppose a single-qubit error occurs on
the encoded quantum register. A single-qubit error is in the set 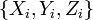 where
where 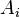 denotes a Pauli error on qubit
denotes a Pauli error on qubit  .
It is straightforward to verify that any arbitrary single-qubit error has a
unique syndrome. The receiver corrects any single-qubit error by identifying
the syndrome and applying a corrective operation.
.
It is straightforward to verify that any arbitrary single-qubit error has a
unique syndrome. The receiver corrects any single-qubit error by identifying
the syndrome and applying a corrective operation.
References
- D. Gottesman, "Stabilizer codes and quantum error correction," quant-ph/9705052, Caltech Ph.D. thesis. http://arxiv.org/abs/quant-ph/9705052
- P. W. Shor, “Scheme for reducing decoherence in quantum computer memory,” Phys. Rev. A, vol. 52, no. 4, pp. R2493–R2496, Oct 1995.
- A. R. Calderbank and P. W. Shor, “Good quantum error-correcting codes exist,” Phys. Rev. A, vol. 54, no. 2, pp. 1098–1105, Aug 1996. Available at http://arxiv.org/abs/quant-ph/9512032
- A. M. Steane, “Error correcting codes in quantum theory,” Phys. Rev. Lett., vol. 77, no. 5, pp. 793–797, Jul 1996.
- A. Calderbank, E. Rains, P. Shor, and N. Sloane, “Quantum error correction via codes over GF(4),” IEEE Trans. Inf. Theory, vol. 44, pp. 1369–1387, 1998. Available at http://arxiv.org/abs/quant-ph/9608006
| ||||||||||||||||||||||||||||||||||||||||||||||
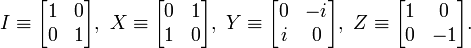
![\Pi^{n}=\left\{
\begin{array}
[c]{c}
e^{i\phi}A_{1}\otimes\cdots\otimes A_{n}:\forall j\in\left\{ 1,\ldots
,n\right\} A_{j}\in\Pi,\ \ \phi\in\left\{ 0,\pi/2,\pi,3\pi/2\right\}
\end{array}
\right\} .](../I/m/7a54a62f55351ebae01d726de1c0b063.png)
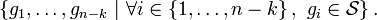
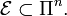
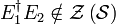
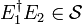
![\left[ A\right] =\left\{ \beta A\ |\ \beta\in\mathbb{C},\ \left\vert
\beta\right\vert =1\right\} .](../I/m/00add670408a76d89555ceb0ec177cf1.png)
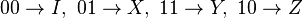
![\left[ N\left( u+v\right) \right] =\left[ N\left( u\right) \right]
\left[ N\left( v\right) \right] .](../I/m/34d051b8b258b3c8ac74e447ca3ddeaf.png)
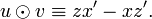
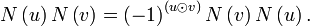
![\left[ \mathbf{A}\right] =\left\{ \beta\mathbf{A}\ |\ \beta\in
\mathbb{C},\ \left\vert \beta\right\vert =1\right\} .](../I/m/89f145bb0c282a546504f3a1a91ae781.png)
![\left[ \mathbf{A}\right] \ast\left[ \mathbf{B}\right] \equiv\left[
A_{1}\right] \ast\left[ B_{1}\right] \otimes\cdots\otimes\left[
A_{n}\right] \ast\left[ B_{n}\right] =\left[ A_{1}B_{1}\right] \otimes\cdots\otimes\left[ A_{n}B_{n}\right]
=\left[ \mathbf{AB}\right] .](../I/m/fad33c795c8368f0e7dd7c443ad64b4f.png)
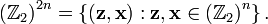
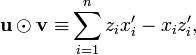
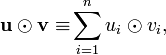
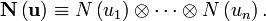
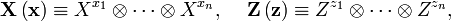
![\left[ \mathbf{N}\left( \mathbf{u}\right) \right] =\left[ \mathbf{Z}
\left( \mathbf{z}\right) \mathbf{X}\left( \mathbf{x}\right) \right] .](../I/m/0f340def5f6a649a2d091edf896a8e2c.png)
![\left[ \mathbf{N}\left( \mathbf{u+v}\right) \right] =\left[
\mathbf{N}\left( \mathbf{u}\right) \right] \left[ \mathbf{N}\left(
\mathbf{v}\right) \right] ,](../I/m/4cffab8f2ba98b46c43a111634b0a656.png)
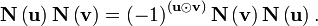
![\begin{array}
[c]{ccccccc}
g_{1} & = & X & Z & Z & X & I\\
g_{2} & = & I & X & Z & Z & X\\
g_{3} & = & X & I & X & Z & Z\\
g_{4} & = & Z & X & I & X & Z
\end{array}](../I/m/0515706027c8207f61ca8b758fe8192e.png)