Stability derivatives

 indicates the changes are in response to changes in angle of attack. This stability derivative is pronounced "see-em-alpha". It is one measure of how strongly an aircraft wants to fly "nose first", which is clearly very important.
indicates the changes are in response to changes in angle of attack. This stability derivative is pronounced "see-em-alpha". It is one measure of how strongly an aircraft wants to fly "nose first", which is clearly very important.
Stability Derivatives, and also Control Derivatives, are measures of how particular forces and moments on an aircraft change as other parameters related to stability change (parameters such as airspeed, altitude, angle of attack, etc.). For a defined "trim" flight condition, changes and oscillations occur in these parameters. Equations of motion are used to analyze these changes and oscillations. Stability and control derivatives are used to linearize (simplify) these equations of motion so the stability of the vehicle can be more readily analyzed.
Stability and control derivatives change as flight conditions change. The collection of stability and control derivatives as they change over a range of flight conditions is called an Aero Model. Aero models are used in engineering flight simulators to analyze stability, and in real-time flight simulators for training and entertainment.
Stability derivative vs. Control derivative
Stability derivatives and Control derivatives are related because they both are measures of forces and moments on a vehicle as other parameters change. Often the words are used together and abbreviated in the term "S&C derivatives". They differ in that stability derivatives measure the effects of changes in flight conditions while control derivatives measure effects of changes in the control surface positions:
- A stability derivative measures how much change occurs in a force or moment acting on the vehicle when there is a small change in a flight condition parameter such as angle of attack, airspeed, altitude, etc. (Such parameters are called "states".)
- A control derivative measures how much change occurs in a force or moment acting on the vehicle when there is a small change in the deflection of a control surface such as the ailerons, elevator, and rudder.
Uses
Linearization (simplification) of stability analysis
Stability and control derivatives change as flight conditions change. That is, the forces and moments on the vehicle are seldom simple (linear) functions of its states. Because of this, the dynamics of atmospheric flight vehicles can be difficult to analyze. The following are two methods used to tackle this complexity.
- Small oscillations about otherwise steady flight conditions
- One way to simplify analysis is to consider only small oscillations about otherwise steady flight conditions. The set of flight conditions (such as altitude, airspeed, angle of attack) are called "trim" conditions when they are steady and not changing. When flight conditions are steady, stability and control derivatives are constant and can be more easily analyzed mathematically. The analysis at a single set of flight conditions is then applied to a range of different flight conditions.
- Application in simulators for stability analysis
- In a flight simulator, it is possible to "look up" new values for stability and control derivatives as conditions change. And so, the "linear approximations" aren't as great and stability can be assessed in maneuvers that span a greater range of flight conditions. Flight simulators used for analysis such as this are called "engineering simulators". The set of values for stability and control derivatives (as they change over various flight conditions) is called an Aero Model.
Use in flight simulators
In addition to engineering simulators, aero models are often used in real time flight simulators for home use and professional flight training.
Names for the axes of vehicles
Air vehicles use a coordinate system of axes to help name important parameters used in the analysis of stability. All the axes run through the center of gravity (called the "CG"):
- "X" or "x" axis runs from back to front along the body, called the Roll Axis.
- "Y" or "y" axis runs left to right along the wing, called the Pitch Axis.
- "Z" or "z" runs from top to bottom, called the Yaw Axis.
Two slightly different alignments of these axes are used depending on the situation: "Body-fixed Axes", and "Stability Axes".
Body-fixed Axes
Body-fixed axes, or "Body Axes", are defined and fixed relative to the body of the vehicle.:[1]
- X body axis is aligned along the vehicle body and is usually positive toward the normal direction of motion.
- Y body axis is at a right angle to the x body axis and is oriented along the wings of the vehicle. If there are no wings (as with a missile), a "horizontal" direction is defined in a way that is useful. The Y body axis is usually taken to be positive to right side of the vehicle.
- Z body axis is perpendicular to wing-body (XY) plane and usually points downward.
Stability Axes
Aircraft (usually not missiles) operate at a nominally constant "trim" angle of attack. The angle of the nose (the X Axis) does not align with the direction of the oncoming air. The difference in these directions is the angle of attack. So, for many purposes, parameters are defined in terms of a slightly modified axis system called "stability axes". The stability axis system is used to get the X axis aligned with the oncoming flow direction. Essentially, the body axis system is rotated about the Y body axis by the trim angle of attack and then "re-fixed" to the body of the aircraft:[1]
- X stability axis is aligned into the direction of the oncoming air in steady flight. (It is projected into the plane made by the X and Z body axes if there is sideslip).
- Y stability axis is the same as the Y body-fixed axis.
- Z stability axis is perpendicular to the plane made by the X stability axis and the Y body axis.
Names for Forces, Moments, and Velocities
Forces and velocities along each of the axes
Forces on the vehicle along the body axes are called "Body-axis Forces":
- X, or FX, is used to indicate forces on the vehicle along the X axis
- Y, or FY, is used to indicate forces on the vehicle along the Y axis
- Z, or FZ, is used to indicate forces on the vehicle along the Z axis
- u (lower case) is used for speed of the oncoming flow along the X body axis
- v (lower case) is used for speed of the oncoming flow along the Y body axis
- w (lower case) is used for speed of the oncoming flow along the Z body axis
- It is helpful to think of these speeds as projections of the relative wind vector on to the three body axes, rather than in terms of the translational motion of the vehicle relative to the fluid. As the body rotates relative to direction of the relative wind, these components change, even when there is no net change in speed.
Moments and angular rates around each of the axes
- L is used to indicate the "rolling moment", which is around the X axis. Whether it is around the X body axis or the X stability axis depends on context (such as a subscript).
- M is used to indicate the name of the "pitching moment", which is around the Y axis.
- N is used to indicate the name of the "yawing moment", which is around the Z axis. Whether it is around the Z body axis or the Z stability axis depends on context (such as a subscript).
- "P" or "p" is used for angular rate about the X axis ("Roll rate about the roll axis"). Whether it is around the X body axis or the X stability axis depends on context (such as a subscript).
- "Q" or "q" is used for angular rate about the Y axis ("Pitch rate about the pitch axis").
- "R" or "r" is used for angular rate about the Z axis ("Yaw rate about the yaw axis"). Whether it is around the Z body axis or the Z stability axis depends on context (such as a subscript).
Equations of Motion
The use of stability derivatives is most conveniently demonstrated with missile or rocket configurations, because these exhibit greater symmetry than aeroplanes, and the equations of motion are correspondingly simpler. If it is assumed that the vehicle is roll-controlled, the pitch and yaw motions may be treated in isolation. It is common practice to consider the yaw plane, so that only 2D motion need be considered. Furthermore, it is assumed that thrust equals drag, and the longitudinal equation of motion may be ignored.

The body is oriented at angle 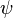 (psi) with respect to inertial axes. The body is oriented at an angle
(psi) with respect to inertial axes. The body is oriented at an angle  (beta) with respect to the velocity vector, so that the components of velocity in body axes are:
(beta) with respect to the velocity vector, so that the components of velocity in body axes are:
where U is the speed.
The aerodynamic forces are generated with respect to body axes, which is not an inertial frame. In order to calculate the motion, the forces must be referred to inertial axes. This requires the body components of velocity to be resolved through the heading angle 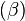 into inertial axes.
into inertial axes.
Resolving into fixed (inertial) axes:
The acceleration with respect to inertial axes is found by differentiating these components of velocity with respect to time:
From Newton's Second Law, this is equal to the force acting divided by the mass. Now forces arise from the pressure distribution over the body, and hence are generated in body axes, and not in inertial axes, so the body forces must be resolved to inertial axes, as Newton's Second Law does not apply in its simplest form to an accelerating frame of reference.
Resolving the body forces:
Newton's Second Law, assuming constant mass:
where m is the mass. Equating the inertial values of acceleration and force, and resolving back into body axes, yields the equations of motion:
The sideslip,  , is a small quantity, so the small perturbation equations of motion become:
, is a small quantity, so the small perturbation equations of motion become:
The first resembles the usual expression of Newton's Second Law, whilst the second is essentially the centrifugal acceleration. The equation of motion governing the rotation of the body is derived from the time derivative of angular momentum:
where C is the moment of inertia about the yaw axis.
Assuming constant speed, there are only two state variables;  and
and  , which will be written more compactly as the yaw rate r.
There is one force and one moment, which for a given flight condition will each be functions of
, which will be written more compactly as the yaw rate r.
There is one force and one moment, which for a given flight condition will each be functions of  , r and their time derivatives. For typical missile configurations the forces and moments depend, in the short term, on
, r and their time derivatives. For typical missile configurations the forces and moments depend, in the short term, on  and r. The forces may be expressed in the form:
and r. The forces may be expressed in the form:
where 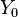 is the force corresponding to the equilibrium condition (usually called the trim) whose stability is being investigated.
It is common practice to employ a shorthand:
is the force corresponding to the equilibrium condition (usually called the trim) whose stability is being investigated.
It is common practice to employ a shorthand:
The partial derivative  and all similar terms characterising the increments in forces and moments due to increments in the state variables are called stability derivatives.
Typically,
and all similar terms characterising the increments in forces and moments due to increments in the state variables are called stability derivatives.
Typically,  is insignificant for missile configurations, so the equations of motion reduce to:
is insignificant for missile configurations, so the equations of motion reduce to:
Stability Derivative Contributions
Each stability derivative is determined by the position, size, shape and orientation of the missile components. In aircraft, the directional stability determines such features as dihedral of the main planes, size of fin and area of tailplane, but the large number of important stability derivatives involved precludes a detailed discussion within this article. The missile is characterised by only three stability derivatives, and hence provides a useful introduction to the more complex aeroplane dynamics.

Consider first 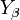 , a body at an angle of attack
, a body at an angle of attack  generates a lift force in the opposite direction to the motion of the body. For this reason
generates a lift force in the opposite direction to the motion of the body. For this reason 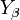 is always negative.
is always negative.

At low angles of attack, the lift is generated primarily by the wings, fins and the nose region of the body. The total lift acts at a distance  ahead of the centre of gravity (it has a negative value in the figure), this, in missile parlance, is the centre of pressure . If the lift acts ahead of the centre of gravity, the yawing moment will be negative, and will tend to increase the angle of attack, increasing both the lift and the moment further. It follows that the centre of pressure must lie aft of the centre of gravity for static stability.
ahead of the centre of gravity (it has a negative value in the figure), this, in missile parlance, is the centre of pressure . If the lift acts ahead of the centre of gravity, the yawing moment will be negative, and will tend to increase the angle of attack, increasing both the lift and the moment further. It follows that the centre of pressure must lie aft of the centre of gravity for static stability.  is the static margin and must be negative for longitudinal static stability. Alternatively, positive angle of attack must generate positive yawing moment on a statically stable missile, i.e.
is the static margin and must be negative for longitudinal static stability. Alternatively, positive angle of attack must generate positive yawing moment on a statically stable missile, i.e. 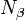 must be positive. It is common practice to design manoeuvrable missiles with near zero static margin (i.e. neutral static stability).
must be positive. It is common practice to design manoeuvrable missiles with near zero static margin (i.e. neutral static stability).
The need for positive 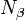 explains why arrows and darts have flights and unguided rockets have fins.
explains why arrows and darts have flights and unguided rockets have fins.

The effect of angular velocity is mainly to decrease the nose lift and increase the tail lift, both of which act in a sense to oppose the rotation. 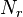 is therefore always negative. There is a contribution from the wing, but since missiles tend to have small static margins (typically less than a calibre), this is usually small. Also the fin contribution is greater than that of the nose, so there is a net force
is therefore always negative. There is a contribution from the wing, but since missiles tend to have small static margins (typically less than a calibre), this is usually small. Also the fin contribution is greater than that of the nose, so there is a net force  , but this is usually insignificant compared with
, but this is usually insignificant compared with 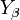 and is usually ignored.
and is usually ignored.
Response
Manipulation of the equations of motion yields a second order homogeneous linear differential equation in the angle of attack  :
:
The qualitative behavior of this equation is considered in the article on directional stability. Since 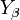 and
and 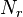 are both negative, the damping is positive. The stiffness does not only depend on the static stability term
are both negative, the damping is positive. The stiffness does not only depend on the static stability term 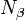 , it also contains a term which effectively determines the angle of attack due to the body rotation. The distance of the center of lift, including this term, ahead of the centre of gravity is called the maneuver margin. It must be negative for stability.
, it also contains a term which effectively determines the angle of attack due to the body rotation. The distance of the center of lift, including this term, ahead of the centre of gravity is called the maneuver margin. It must be negative for stability.
This damped oscillation in angle of attack and yaw rate, following a disturbance, is called the 'weathercock' mode, after the tendency of a weathercock to point into wind.
Comments
The state variables were chosen to be the angle of attack  and the yaw rate r, and have omitted the speed perturbation u, together with the associated derivatives e.g.
and the yaw rate r, and have omitted the speed perturbation u, together with the associated derivatives e.g.  . This may appear arbitrary. However, since the timescale of the speed variation is much greater than that of the variation in angle of attack, its effects are negligible as far as the directional stability of the vehicle is concerned. Similarly, the effect of roll on yawing motion was also ignored, because missiles generally have low aspect ratio configurations and the roll inertia is much less than the yaw inertia, consequently the roll loop is expected to be much faster than the yaw response, and is ignored. These simplifications of the problem based on a priori knowledge, represent an engineer's approach. Mathematicians prefer to keep the problem as general as possible and only simplify it at the end of the analysis, if at all.
. This may appear arbitrary. However, since the timescale of the speed variation is much greater than that of the variation in angle of attack, its effects are negligible as far as the directional stability of the vehicle is concerned. Similarly, the effect of roll on yawing motion was also ignored, because missiles generally have low aspect ratio configurations and the roll inertia is much less than the yaw inertia, consequently the roll loop is expected to be much faster than the yaw response, and is ignored. These simplifications of the problem based on a priori knowledge, represent an engineer's approach. Mathematicians prefer to keep the problem as general as possible and only simplify it at the end of the analysis, if at all.
Aircraft dynamics is more complex than missile dynamics, mainly because the simplifications, such as separation of fast and slow modes, and the similarity between pitch and yaw motions, are not obvious from the equations of motion, and are consequently deferred until a late stage of the analysis. Subsonic transport aircraft have high aspect ratio configurations, so that yaw and roll cannot be treated as decoupled. However, this is merely a matter of degree; the basic ideas needed to understand aircraft dynamics are covered in this simpler analysis of missile motion.
Control Derivatives
Deflection of control surfaces modifies the pressure distribution over the vehicle, and these are dealt with by including perturbations in forces and moments due to control deflection. The fin deflection is normally denoted  (zeta). Including these terms, the equations of motion become:
(zeta). Including these terms, the equations of motion become:
Including the control derivatives enables the response of the vehicle to be studied, and the equations of motion used to design the autopilot.
Examples
- CL
 , called Dihedral Effect, is a stability derivative that measures changes in rolling moment as Angle of sideslip changes. The "L" indicates rolling moment and the
, called Dihedral Effect, is a stability derivative that measures changes in rolling moment as Angle of sideslip changes. The "L" indicates rolling moment and the  indicates sideslip angle.
indicates sideslip angle.
See also
- Longitudinal static stability
- Neutral point
- Aerodynamic center
- Flight dynamics
- Directional Stability
References
- Babister A W: Aircraft Dynamic Stability and Response. Elsever 1980, ISBN 0-08-024768-7
- Friedland B: Control System Design. McGraw-Hill Book Company 1987. ISBN 0-07-100420-3
- Roskam Jan: Airplane Flight Dynamics and Automatic Flight Controls. Roskam Aviation and Engineering Corporation 1979. Second Printing 1982. Library of Congress Catalog Card Number: 78-31382.





















