Spread option

In finance, a spread option is a type of option where the payoff is based on the difference in price between two underlying assets. For example the two assets could be crude oil and heating oil; trading such an option might be of interest to oil refineries, whose profits are a function of the difference between these two prices. Spread options are generally traded over the counter, rather than on exchange.^[1][2]

A 'spread option' is not the same as an 'option spread'. A spread option is a new, relatively rare type of exotic option on two underlyings, while an option spread is a combination trade: the purchase of one (vanilla) option and the sale of another option on the same underlying.

Spread option valuation

For a spread call, the payoff can be written as 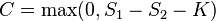where S1 and S2 are the prices of the two assets and K is a constant called the strike price. For a spread put it is .

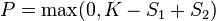When K equals zero a spread option is the same as an option to exchange one asset for another. An explicit solution, Margrabe's formula, is available in this case.

In 1995 Kirk's Approximation,^[3] a formula valid when K is small but non-zero was published. This amounts to a modification of the standard Black-Scholes formula, with a special expression for the sigma (volatility) to be used, which is based on the volatilities and the correlation of the two assets.

The same year Pearson published an algorithm^[4] requiring a single numerical integration to compute the option value.

This method was improved upon in 2006 when Li, Deng and Zhou^[5] published accurate approximation formulas for both spread option prices and their Greeks.

References