Spitzer resistivity

Spitzer resistivity is a classical model of electrical resistivity, 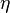\eta, that is based upon electron ion collisions.[1][2] It is given by

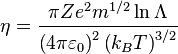
\eta =\dfrac {\pi Ze^{2}m^{1/2}\ln \Lambda } {\left( 4\pi \varepsilon_{0}\right) ^{2}\left( k_{B}T\right)^{3/2}}

where Z is the ionization of nuclei, m is the electron mass, ε0 is the electric permittivity of free space, lnΛ is the Coulomb logarithm, kB is Boltzmann's constant and T is the temperature in kelvins.

This resistivity model was proposed by Lyman Spitzer.[3]

Spitzer resistivity is commonly used in plasma physics.[2]

References

  1. ↑ Trintchouk, Fedor, Yamada, M, Ji, H, Kulsrud, RM, Carter, TA (2003). "Measurement of the transverse Spitzer resistivity during collisional magnetic reconnection". Physics of Plasmas 10: 319. doi:10.1063/1.1528612.
  2. ↑ 2.0 2.1 Davies, JR (2003). "Electric and magnetic field generation and target heating by laser-generated fast electrons". Physical Review E (APS) 68 (5): 056404. doi:10.1103/physreve.68.056404.
  3. ↑ Forest, CB, Kupfer, K, Luce, TC, Politzer, PA, Lao, LL, Wade, MR, Whyte, DG, Wroblewski, D (1994). "Determination of the noninductive current profile in tokamak plasmas". Physical review letters (APS) 73 (18): 2444. doi:10.1103/physrevlett.73.2444.

External links