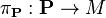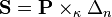Spinor field

In differential geometry, given a spin structure on a n-dimensional Riemannian manifold (M, g) a section of the spinor bundle S is called a spinor field. The complex vector bundle

\pi_{\mathbf S}:{\mathbf S}\to M\,

is associated to the corresponding principal bundle

\pi_{\mathbf P}:{\mathbf P}\to M\,

of spin frames over M via the spin representation of its structure group Spin(n) on the space of spinors Δ_n.

Formal definition

Let (P, F_P) be a spin structure on a Riemannian manifold (M, g) that is, an equivariant lift of the oriented orthonormal frame bundle 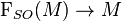$\mathrm F_{SO}(M)\to M$ with respect to the double covering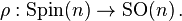 $\rho: {\mathrm {Spin}}(n)\to {\mathrm {SO}}(n)\,.$

One usually defines the spinor bundle^[1] 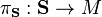$\pi_{\mathbf S}:{\mathbf S}\to M\,$ to be the complex vector bundle

{\mathbf S}={\mathbf P}\times_{\kappa}\Delta_n\,

associated to the spin structure P via the spin representation 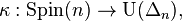$\kappa: {\mathrm {Spin}}(n)\to {\mathrm U}(\Delta_n),\,$ where U(W) denotes the group of unitary operators acting on a Hilbert space W.

A spinor field is defined to be a section of the spinor bundle S, i.e., a smooth mapping 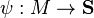$\psi : M \to {\mathbf S}\,$ such that 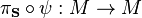$\pi_{\mathbf S}\circ\psi: M\to M\,$ is the identity mapping id_M of M.

Notes

↑ Friedrich, Thomas (2000), Dirac Operators in Riemannian Geometry, p. 53

Books

Lawson, H. Blaine; Michelsohn, Marie-Louise (1989). Spin Geometry. Princeton University Press. ISBN 978-0-691-08542-5.
Friedrich, Thomas (2000), Dirac Operators in Riemannian Geometry, American Mathematical Society, ISBN 978-0-8218-2055-1

Spinor field

Formal definition

See also

Notes

Books