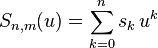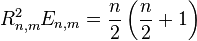Spherium
The "spherium" model consists of two electrons trapped on the surface of a sphere of radius  . It has been used by Berry and collaborators [1] to understand both weakly and strongly correlated systems and to suggest an "alternating" version of Hund's rule. Seidl studies this system in the context of density functional theory (DFT) to develop new correlation functionals within the adiabatic connection.[2]
. It has been used by Berry and collaborators [1] to understand both weakly and strongly correlated systems and to suggest an "alternating" version of Hund's rule. Seidl studies this system in the context of density functional theory (DFT) to develop new correlation functionals within the adiabatic connection.[2]
The electronic Hamiltonian in atomic units is
where  is the interelectronic distance.
For the singlet S states, it can be then shown[3] that the wave function
is the interelectronic distance.
For the singlet S states, it can be then shown[3] that the wave function 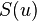 satisfies the Schrödinger equation
satisfies the Schrödinger equation
By introducing the dimensionless variable 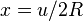 , this becomes a Heun equation with singular points at
, this becomes a Heun equation with singular points at 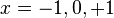 . Based on the known solutions of the Heun equation, we seek wave functions of the form
. Based on the known solutions of the Heun equation, we seek wave functions of the form
and substitution into the previous equation yields the recurrence relation
with the starting values 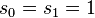 . Thus, the Kato cusp condition is
. Thus, the Kato cusp condition is
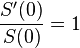 .
.
The wave function reduces to the polynomial
(where  the number of roots between
the number of roots between  and
and 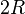 ) if, and only if,
) if, and only if, 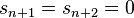 . Thus, the energy
. Thus, the energy 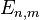 is a root of the polynomial equation
is a root of the polynomial equation 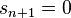 (where
(where  ) and the corresponding radius
) and the corresponding radius 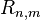 is found from the previous equation which yields
is found from the previous equation which yields
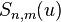 is the exact wave function of the
is the exact wave function of the  -th excited state of singlet S symmetry for the radius
-th excited state of singlet S symmetry for the radius 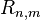 .
.
We know from the work of Loos and Gill [3] that the HF energy of the lowest singlet S state is 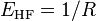 . It follows that the exact correlation energy for
. It follows that the exact correlation energy for 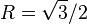 is
is 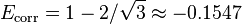 which is much larger than the limiting correlation energies of the helium-like ions (
which is much larger than the limiting correlation energies of the helium-like ions (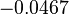 ) or Hooke's atoms (
) or Hooke's atoms (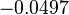 ). This confirms the view that electron correlation on the surface of a sphere is qualitatively different from that in three-dimensional physical space.
). This confirms the view that electron correlation on the surface of a sphere is qualitatively different from that in three-dimensional physical space.
Spherium on a 3-Sphere
Recent work by Loos et al.[4] considered the case of two electrons confined to a 3-sphere repelling Coulombically. They report a ground state energy of (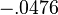 ).
).
See also
References
- ↑ Ezra, G. S.; Berry, R. S. (1982), Physical Review A 25: 1513, Bibcode:1982PhRvA..25.1513E, doi:10.1103/PhysRevA.25.1513 Missing or empty
|title=(help) - ↑ Seidl, M. (2007), Physical Review A 75: 062506, Bibcode:2007PhRvA..75a2506P, doi:10.1103/PhysRevA.75.012506 Missing or empty
|title=(help) - ↑ 3.0 3.1 Loos, P.-F.; Gill, P. M. W. (2009), Physical Review A 79: 062517, arXiv:1002.3398, Bibcode:2009PhRvA..79f2517L, doi:10.1103/PhysRevA.79.062517 Missing or empty
|title=(help) - ↑ Loos, P.-F.; Gill, P. M. W. (2010), Molecular Physics 108: 2527, arXiv:1004.3641, Bibcode:2010MolPh.108.2527L, doi:10.1080/00268976.2010.508472 Missing or empty
|title=(help)
Further reading
- Loos, P.-F.; Gill, P. M. W. (2009), "Two electrons on a hypersphere: a quasiexactly solvable model", Physical Review Letters 103: 123008, arXiv:1002.3400, Bibcode:2009PhRvL.103l3008L, doi:10.1103/physrevlett.103.123008
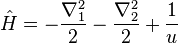
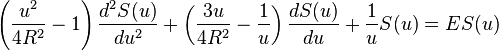
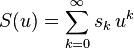
![s_{k+2} = \frac{ s_{k+1} + \left[ k(k+2) \frac{1}{4R^2} - E \right] s_k }{(k+2)^2}](../I/m/c75acde00c77c9f9ec0a6ea457a52514.png)