Sphere theorem (3-manifolds)
In mathematics, in the topology of 3-manifolds, the sphere theorem of Papakyriakopoulos (1957) gives conditions for elements of the second homotopy group of a 3-manifold to be represented by embedded spheres.
One example is the following:
Let  be an orientable 3-manifold such that
be an orientable 3-manifold such that 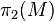 is not the trivial group. Then there exists a non-zero element of
is not the trivial group. Then there exists a non-zero element of
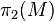 having a representative that is an embedding
having a representative that is an embedding 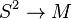 .
.
The proof of this version can be based on transversality methods, see Batude below.
Another more general version (also called the projective plane theorem due to Epstein) is:
Let  be any 3-manifold and
be any 3-manifold and  a
a 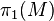 -invariant subgroup of
-invariant subgroup of 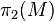 . If
. If 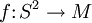 is a general position map such that
is a general position map such that ![[f]\notin N](../I/m/464d68d51a4ca9db0a18d04549f99ed0.png) and
and  is any neighborhood of the singular set
is any neighborhood of the singular set 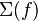 , then there is a map
, then there is a map 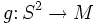 satisfying
satisfying
![[g]\notin N](../I/m/4d762ecd1d92c44c441ab01a84f98a6b.png) ,
,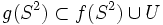 ,
,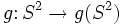 is a covering map, and
is a covering map, and 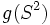 is a 2-sided submanifold (2-sphere or projective plane) of
is a 2-sided submanifold (2-sphere or projective plane) of  .
.
quoted in Hempel (p. 54)
References
- Batude, J. L. (1971). "Singularité générique des applications différentiables de la 2-sphère dans une 3-variété différentiable". Annales de l'Institut Fourier 21 (3): 151–172.
- Epstein, D. B. A. (1961). "Projective planes in 3-manifolds". Proceedings of the London Mathematical Society, III Ser. 11 (1): 469–484. doi:10.1112/plms/s3-11.1.469.
- Hempel, J. (1978). 3-manifolds. Princeton University Press.
- C. Papakyriakopoulos (1957). "On Dehn's lemma and asphericity of knots". Annals of Mathematics (Annals of Mathematics) 66 (1): 1–26. doi:10.2307/1970113. JSTOR 1970113.
- Whitehead, J. H. C. (1958). "On 2-spheres in 3-manifolds". Bulletin of the American Mathematical Society 64 (4): 161–166. doi:10.1090/S0002-9904-1958-10193-7.