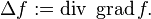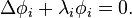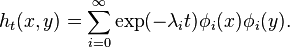Spectral shape analysis
Spectral shape analysis relies on the spectrum (eigenvalues and/or eigenfunctions) of the Laplace–Beltrami operator to compare and analyze geometric shapes. Since the spectrum of the Laplace–Beltrami operator is invariant under isometries, it is well suited for the analysis or retrieval of non-rigid shapes, i.e. bendable objects such as humans, animals, plants, etc.
Laplace
The Laplace–Beltrami operator is involved in many important differential equations, such as the heat equation and the wave equation. It can be defined on a Riemannian manifold as the divergence of the gradient of a real-valued function f:
Its spectral components can be computed by solving the Helmholtz equation (or Laplacian eigenvalue problem):
The solutions are the eigenfunctions 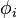 (modes) and corresponding eigenvalues
(modes) and corresponding eigenvalues 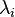 , representing a diverging sequence of positive real numbers. The first eigenvalue is zero for closed domains or when using the Neumann boundary condition. For some shapes, the spectrum can be computed analytically (e.g. rectangle, flat torus, cylinder, disk or sphere). For the sphere, for example, the eigenfunctions are the spherical harmonics.
, representing a diverging sequence of positive real numbers. The first eigenvalue is zero for closed domains or when using the Neumann boundary condition. For some shapes, the spectrum can be computed analytically (e.g. rectangle, flat torus, cylinder, disk or sphere). For the sphere, for example, the eigenfunctions are the spherical harmonics.
The most important properties of the eigenvalues and eigenfunctions are that they are isometry invariants. In other words, if the shape is not stretched (e.g. a sheet of paper bent into the third dimension), the spectral values will not change. Bendable objects, like animals, plants and humans, can move into different body postures with only minimal stretching at the joints. The resulting shapes are called near-isometric and can be compared using spectral shape analysis. However, the isometric deformation of surfaces in 3D in the strict sense are rigid transformations. To characterize the actual deformation undergoing for the interest of nonrigid shape analysis, smooth deformations are introduced as an alternative family of deformation to isometry, where eigenvalues are allowed to perturb with finite error bounds.[1]
Discretizations
Geometric shapes are often represented as 2D curved surfaces, 2D surface meshes (usually triangle meshes) or 3D solid objects (e.g. using voxels or tetrahedra meshes). The Helmholtz equation can be solved for all these cases. If a boundary exists, e.g. a square, or the volume of any 3D geometric shape, boundary conditions need to be specified.
Several discretizations of the Laplace operator exist (see Discrete Laplace operator) for the different types of geometry representations. Many of these operators do not approximate well the underlying continuous operator.
Spectral shape descriptors
ShapeDNA and its variants
The ShapeDNA is one of the first spectral shape descriptors. It is the normalized beginning sequence of the eigenvalues of the Laplace–Beltrami operator.[2][3] Its main advantages are the simple representation (a vector of numbers) and comparison, scale invariance, and in spite of its simplicity a very good performance for shape retrieval of non-rigid shapes.[4] Competitors of shapeDNA include singular values of Geodesic Distance Matrix (SD-GDM) [5] and Reduced BiHarmonic Distance Matrix (R-BiHDM).[1] However, the eigenvalues are a global descriptor, therefore the shapeDNA and other global spectral descriptors cannot be used for local or partial shape analysis.
Global point signature (GPS)
The global point signature[6] at a point  is a vector of scaled eigenfunctions of the Laplace–Beltrami operator computed at
is a vector of scaled eigenfunctions of the Laplace–Beltrami operator computed at  (i.e. the spectral embedding of the shape). The GPS is a global feature in the sense that it cannot be used for partial shape matching.
(i.e. the spectral embedding of the shape). The GPS is a global feature in the sense that it cannot be used for partial shape matching.
Heat kernel signature (HKS)
The heat kernel signature[7] makes use of the eigen-decomposition of the heat kernel:
For each point on the surface the diagonal of the heat kernel 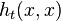 is sampled at specific time values
is sampled at specific time values 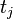 and yields a local signature that can also be used for partial matching or symmetry detection.
and yields a local signature that can also be used for partial matching or symmetry detection.
Spectral Matching
The spectral decomposition of the graph Laplacian associated with complex shapes (see Discrete Laplace operator) provides eigenfunctions (modes) which are invariant to isometries. Each vertex on the shape could be uniquely represented with a combinations of the eigenmodal values at each point, sometimes called spectral coordinates:
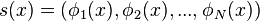 for vertex
for vertex  .
.
Spectral matching consists of establishing the point correspondences by pairing vertices on different shapes that have the most similar spectral coordinates. Early work [8][9][10] focused on sparse correspondences for stereoscopy. Computational efficiency now enables dense correspondences on full meshes, for instance between cortical surfaces.[11] Spectral matching could also be used for complex non-rigid image registration, which is notably difficult when images have very large deformations.[12] Such image registration methods based on spectral eigenmodal values indeed capture global shape characteristics, and contrast with conventional non-rigid image registration methods which are often based on local shape characteristics (e.g., image gradients).
References
- ↑ 1.0 1.1 Ye, J. and Yu, Y. (2015). "A fast modal space transform for robust nonrigid shape retrieval". The Visual Computer, Springer. doi:10.1007/s00371-015-1071-5.
- ↑ Reuter, M. and Wolter, F.-E. and Peinecke, N. (2005). "Laplace-Spectra as Fingerprints for Shape Matching". Proceedings of the 2005 ACM Symposium on Solid and Physical Modeling. pp. 101–106.
- ↑ Reuter, M. and Wolter, F.-E. and Peinecke, N. (2006). "Laplace–Beltrami spectra as Shape-DNA of surfaces and solids". Computer-Aided Design 38 (4): 342–366. doi:10.1016/j.cad.2005.10.011.
- ↑ Lian, Z. et al. (2011). "SHREC'11 track: shape retrieval on non-rigid 3D watertight meshes". Proceedings of the Eurographics 2011 Workshop on 3D Object Retrieval (3DOR'11). pp. 79–88. doi:10.2312/3DOR/3DOR11/079-088.
- ↑ Smeets,D. and Fabry,T. and Hermans,J. and Vandermeulen,D. and Suetens,P. (2009). "Isometric deformation modelling for object recognition.". CAIP 2009, LNCS 5702,: 757–765.
- ↑ Rustamov, R.M. (July 4, 2007). "Laplace–Beltrami eigenfunctions for deformation invariant shape representation". Proceedings of the fifth Eurographics symposium on Geometry processing. Eurographics Association. pp. 225–233.
978-3-905673-46-3
- ↑ Sun, J. and Ovsjanikov, M. and Guibas, L. (2009). "A Concise and Provably Informative Multi-Scale Signature-Based on Heat Diffusion". Computer Graphics Forum 28 (5). pp. 1383–1392.
- ↑ Umeyama, S (1988). "An eigendecomposition approach to weighted graph matching problems". IEEE Transactions on Pattern Analysis and Machine Intelligence 10 (5): 695–703. doi:10.1109/34.6778.
- ↑ Scott, GL and Longuet-Higgins, HC (1991). "An algorithm for associating the features of two images". Royal Society Biological Sciences 244 (1309): 21–26. doi:10.1098/rspb.1991.0045.
- ↑ Shapiro, LS and Brady, JM (1992). "Feature-based correspondence: an eigenvector approach". Image and Vision Computing 10 (5): 283–288. doi:10.1016/0262-8856(92)90043-3.
- ↑ Lombaert, H and Grady, L and Polimeni, JR and Cheriet, F (2013). "FOCUSR: Feature Oriented Correspondence using Spectral Regularization - A Method for Precise Surface Matching". IEEE Transactions on Pattern Analysis and Machine Intelligence 35 (9): 2143–2160. doi:10.1109/tpami.2012.276.
- ↑ Lombaert, H and Grady, L and Pennec, X and Ayache, N and Cheriet, F (2014). "Spectral Log-Demons - Diffeomorphic Image Registration with Very Large Deformations". International Journal of Computer Vision 107 (3): 254–271. doi:10.1007/s11263-013-0681-5.