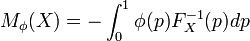Spectral risk measure
A Spectral risk measure is a risk measure given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio returns and outputs the amount of the numeraire (typically a currency) to be kept in reserve. A spectral risk measure is always a coherent risk measure, but the converse does not always hold. An advantage of spectral measures is the way in which they can be related to risk aversion, and particularly to a utility function, through the weights given to the possible portfolio returns.[1]
Definition
Consider a portfolio  Then a spectral risk measure
Then a spectral risk measure 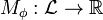 where
where  is non-negative, non-increasing, right-continuous, integrable function defined on
is non-negative, non-increasing, right-continuous, integrable function defined on ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) such that
such that 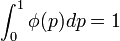 is defined by
is defined by
where 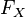 is the cumulative distribution function for X.[2][3]
is the cumulative distribution function for X.[2][3]
If there are  equiprobable outcomes with the corresponding payoffs given by the order statistics
equiprobable outcomes with the corresponding payoffs given by the order statistics 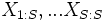 . Let
. Let 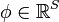 . The measure
. The measure
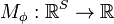 defined by
defined by 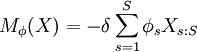 is a spectral measure of risk if
is a spectral measure of risk if 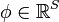 satisfies the conditions
satisfies the conditions
- Nonnegativity:
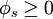 for all
for all 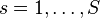 ,
, - Normalization:
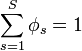 ,
, - Monotonicity :
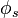 is non-increasing, that is
is non-increasing, that is 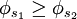 if
if 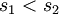 and
and 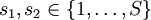 .[4]
.[4]
Properties
Spectral risk measures are also coherent. Every spectral risk measure 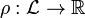 satisfies:
satisfies:
- Positive Homogeneity: for every portfolio X and positive value
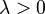 ,
, 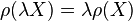 ;
; - Translation-Invariance: for every portfolio X and
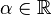 ,
, 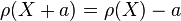 ;
; - Monotonicity: for all portfolios X and Y such that
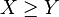 ,
, 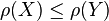 ;
; - Sub-additivity: for all portfolios X and Y,
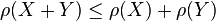 ;
; - Law-Invariance: for all portfolios X and Y with cumulative distribution functions
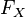 and
and 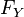 respectively, if
respectively, if 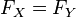 then
then 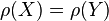 ;
; - Comonotonic Additivity: for every comonotonic random variables X and Y,
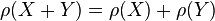 . Note that X and Y are comonotonic if for every
. Note that X and Y are comonotonic if for every 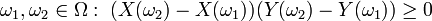 .[2]
.[2]
Examples
- The expected shortfall is a spectral measure of risk.
- The expected value is trivially a spectral measure of risk.
See also
References
- ↑ Cotter, John; Dowd, Kevin (December 2006). "Extreme spectral risk measures: An application to futures clearinghouse margin requirements". Journal of Banking & Finance 30 (12): 3469–3485. doi:10.1016/j.jbankfin.2006.01.008.
- ↑ 2.0 2.1 Adam, Alexandre; Houkari, Mohamed; Laurent, Jean-Paul (2007). "Spectral risk measures and portfolio selection" (pdf). Retrieved October 11, 2011.
- ↑ Dowd, Kevin; Cotter, John; Sorwar, Ghulam (2008). "Spectral Risk Measures: Properties and Limitations" (pdf). CRIS Discussion Paper Series (2). Retrieved October 13, 2011.
- ↑ Acerbi, Carlo (2002), "Spectral measures of risk: A coherent representation of subjective risk aversion", Journal of Banking and Finance (Elsevier) 26 (7): 1505–1518, doi:10.1016/S0378-4266(02)00281-9