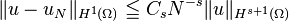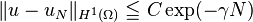Spectral element method

In the numerical solution of partial differential equations, a topic in mathematics, the spectral element method (SEM) is a formulation of the finite element method (FEM) that uses high degree piecewise polynomials as basis functions. The spectral element method was introduced in a 1984 paper^[1] by A. T. Patera.

Discussion

The spectral method expands the solution in trigonometric series, a chief advantage being that the resulting method is of very high order. This approach relies on the fact that trigonometric polynomials are an orthonormal basis for 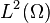. The spectral element method chooses instead a high degree piecewise polynomial basis functions, also achieving a very high order of accuracy. Such polynomials are usually orthogonal Chebyshev polynomials or very high order Legendre polynomials over non-uniformly spaced nodes. In SEM computational error decreases exponentially as the order of approximating polynomial, therefore a fast convergence of solution to the exact solution is realized with fewer degrees of freedom of the structure in comparison with FEM. In structural health monitoring, FEM can be used for detecting large flaws in a structure, but as the size of the flaw is reduced there is a need to use a high frequency wave with a small wavelength. Therefore, the FEM mesh must be much finer, resulting in increased computational time and an inexact solution. SEM, with fewer degrees of freedom per node, can be useful for detecting small flaws. Non-uniformity of nodes helps to make the mass matrix diagonal, which saves time and memory and is also useful for adopting a central difference method (CDM). The disadvantages of SEM include difficulty in modeling complex geometry, compared to the flexibility of FEM.

A-priori error estimate

The classic analysis of Galerkin methods and Céa's lemma holds here and it can be shown that, if u is the solution of the weak equation, u_N is the approximate solution and :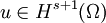

where C is independent from N and s is no larger than the degree of the piecewise polynomial basis. As we increase N, we can also increase the degree of the basis functions. In this case, if u is an analytic function:

where 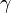depends only on .

Related methods

• G-NI or SEM-NI are the most used spectral methods. The Galerkin formulation of spectral methods or spectral element methods, for G-NI or SEM-NI respectively, is modified and Gaussian numerical integration is used instead of integrals in the definition of the bilinear form 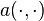and in the functional 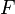. These methods are a family of Petrov–Galerkin methods. Their convergence is a consequence of Strang's lemma.
• The spectral element method uses a tensor product space spanned by nodal basis functions associated with Gauss–Lobatto points. In contrast, the p-version finite element method spans a space of high order polynomials by nodeless basis functions, chosen approximately orthogonal for numerical stability. Since not all interior basis functions need to be present, the p-version finite element method can create a space that contains all polynomials up to a given degree with fewer degrees of freedom.^[2] However, some speedup techniques possible in spectral methods due to their tensor-product character are no longer available. The name p-version means that accuracy is increased by increasing the order of the approximating polynomials (thus, p) rather than decreasing the mesh size, h.
• The hp finite element method (hp-FEM) combines the advantages of the h and p refinements to obtain exponential convergence rates.^[3]

Notes

1. ↑ A. T. Patera. A spectral element method for fluid dynamics - Laminar flow in a channel expansion. Journal of Computational Physics, 54:468--488, 1984.
2. ↑ Barna Szabó and Ivo Babuška, Finite element analysis, John Wiley & Sons, Inc., New York, 1991. ISBN 0-471-50273-1
3. ↑ P. Šolín, K. Segeth, I. Doležel: Higher-order finite element methods, Chapman & Hall/CRC Press, 2003. ISBN 1-58488-438-X