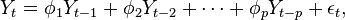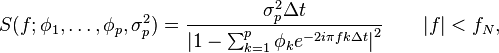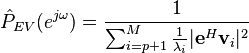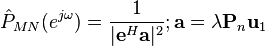Spectral density estimation
In statistical signal processing, the goal of spectral density estimation (SDE) is to estimate the spectral density (also known as the power spectral density) of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
SDE should be distinguished from the field of frequency estimation, which assumes that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seeks to find the location and intensity of the generated frequencies. SDE makes no assumption on the number of components and seeks to estimate the whole generating spectrum.
Techniques
Techniques for spectrum estimation can generally be divided into parametric and non-parametric methods. The parametric approaches assume that the underlying stationary stochastic process has a certain structure which can be described using a small number of parameters (for example, using an auto-regressive or moving average model). In these approaches, the task is to estimate the parameters of the model that describes the stochastic process. By contrast, non-parametric approaches explicitly estimate the covariance or the spectrum of the process without assuming that the process has any particular structure.
Following is a partial list of spectral density estimation techniques:
- Periodogram the basic modulus-squared of the Fourier transform
- Bartlett's method is a periodogram spectral estimate formed by averaging the discrete Fourier transform of multiple segments of the signal to reduce variance of the spectral density estimate
- Welch's method a windowed version of Bartlett's method that uses overlapping segments
- Blackman-Tukey is a periodogram smoothing technique to reduce variance of the spectral density estimate
- Autoregressive moving average estimation, based on fitting to an ARMA model to the time series of signal samples; in addition to ARMA, there are separate moving average and autoregressive methods
- Multitaper is a periodogram-based method that uses multiple tapers, or windows, to form independent estimates of the spectral density to reduce variance of the spectral density estimate
- Maximum entropy spectral estimation is an all-poles method useful for SDE when singular spectral features, such as sharp peaks, are expected.
- Least-squares spectral analysis, based on least squares fitting to known frequencies
- Non-uniform discrete Fourier transform is used when the signal samples are unevenly spaced in time
- Singular spectrum analysis is a nonparametric method that uses a singular value decomposition of the covariance matrix to estimate the spectral density
- Short-time Fourier transform
Parametric estimation
In parametric spectral estimation, one assumes that the signal is modeled by a stationary process which has a spectral density function (SDF) 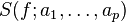 that is a function of the frequency
that is a function of the frequency  and
and  parameters
parameters 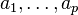 .[1] The estimation problem then becomes one of estimating these parameters.
.[1] The estimation problem then becomes one of estimating these parameters.
The most common form of parametric SDF estimate uses as a model an autoregressive model 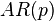 of order
of order  .[1]:392 A signal sequence
.[1]:392 A signal sequence 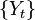 obeying a zero mean
obeying a zero mean 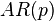 process satisfies the equation
process satisfies the equation
where the 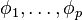 are fixed coefficients and
are fixed coefficients and 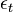 is a white noise process with zero mean and innovation variance
is a white noise process with zero mean and innovation variance 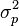 . The SDF for this process is
. The SDF for this process is
with 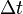 the sampling time interval and
the sampling time interval and 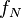 the Nyquist frequency.
the Nyquist frequency.
There are a number of approaches to estimating the parameters 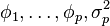 of the
of the 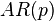 process and thus the spectral density:[1]:452-453
process and thus the spectral density:[1]:452-453
- The Yule-Walker estimators are found by recursively solving the Yule-Walker equations for an
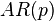 process
process - The Burg estimators are found by treating the Yule-Walker equations as a form of ordinary least squares problem. The Burg estimators are generally considered superior to the Yule-Walker estimators.[1]:452 Burg associated these with maximum entropy spectral estimation.[2]
- The forward-backward least-squares estimators treat the
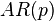 process as a regression problem and solves that problem using forward-backward method. They are competitive with the Burg estimators.
process as a regression problem and solves that problem using forward-backward method. They are competitive with the Burg estimators. - The maximum likelihood estimators assume the white noise is a Gaussian process and estimates the parameters using a maximum likelihood approach. This involves a nonlinear optimization and is more complex than the first three.
Alternative parametric methods include fitting to a moving average model (MA) and to a full autoregressive moving average model (ARMA).
Frequency estimation
Frequency estimation is the process of estimating the complex frequency components of a signal in the presence of noise given assumptions about the number of the components.[3] This contrasts with the general methods above, which do not make prior assumptions about the components.
Finite number of tones
A typical model for a signal  consists of a sum of
consists of a sum of  complex exponentials in the presence of white noise,
complex exponentials in the presence of white noise, 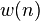
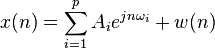 .
.
The power spectral density of  is composed of
is composed of  impulse functions in addition to the spectral density function due to noise.
impulse functions in addition to the spectral density function due to noise.
The most common methods for frequency estimation involve identifying the noise subspace to extract these components. These methods are based on eigen decomposition of the autocorrelation matrix into a signal subspace and a noise subspace. After these subspaces are identified, a frequency estimation function is used to find the component frequencies from the noise subspace. The most popular methods of noise subspace based frequency estimation are Pisarenko's method, the multiple signal classification (MUSIC) method, the eigenvector method, and the minimum norm method.
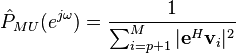 ,
,
Eigenvector method
Minimum norm method
Single tone
If one only wants to estimate the single loudest frequency, one can use a pitch detection algorithm. If the dominant frequency changes over time, then the problem becomes the estimation of the instantaneous frequency as defined in the time–frequency representation. Methods for instantaneous frequency estimation include those based on the Wigner-Ville distribution and higher order ambiguity functions.[4]
If one wants to know all the (possibly complex) frequency components of a received signal (including transmitted signal and noise), one uses a discrete Fourier transform or some other Fourier-related transform.
See also
References
- ↑ 1.0 1.1 1.2 1.3 Donald B. Percival and Andrew T. Walden (1992). Spectral Analysis for Physical Applications. Cambridge University Press. ISBN 9780521435413.
- ↑ Burg, J.P. (1967) "Maximum Entropy Spectral Analysis", Proceedings of the 37th Meeting of the Society of Exploration Geophysicists, Oklahoma City, Oklahoma.
- ↑ Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. ISBN 0-471-59431-8.
- ↑ Lerga, Jonatan. "Overview of Signal Instantaneous Frequency Estimation Methods". University of Rijeka. Retrieved 22 March 2014.
Further reading
- Porat, B. (1994). Digital Processing of Random Signals: Theory & Methods. Prentice Hall. ISBN 0-13-063751-3.
- Priestley, M.B. (1991). Spectral Analysis and Time Series. Academic Press. ISBN 0-12-564922-3.
- P Stoica and R Moses, Spectral Analysis of Signals. Prentice Hall, NJ, 2005 (Chinese Edition, 2007). AVAILABLE FOR DOWNLOAD.
- Thomson, D. J. (1982). "Spectrum estimation and harmonic analysis". Proceedings of the IEEE 70 (9): 1055. doi:10.1109/PROC.1982.12433.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||