Specific detectivity

Specific detectivity, or D*, for a photodetector is a figure of merit used to characterize performance, equal to the reciprocal of noise-equivalent power (NEP), normalized per square root of the sensor's area and frequency bandwidth (reciprocal of twice the integration time).

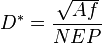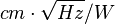Specific detectivity is given by $D^*=\frac{\sqrt{Af}}{NEP}$ , where $A$ is the area of the photosensitive region of the detector and $f$ is the frequency bandwidth. It is commonly expressed in Jones units ( $cm \cdot \sqrt{Hz}/ W$ )in honor of Robert Clark Jones who originally defined it.^[1]^[2]

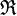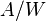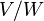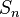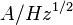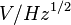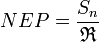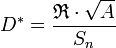Given that noise-equivalent power can be expressed as a function of the responsivity $\mathfrak{R}$ (in units of $A/W$ or $V/W$ ) and the noise spectral density $S_n$ (in units of $A/Hz^{1/2}$ or $V/Hz^{1/2}$ ) as $NEP=\frac{S_n}{\mathfrak{R}}$ , it's common to see the specific detectivity expressed as $D^*=\frac{\mathfrak{R}\cdot\sqrt{A}}{S_n}$ .

It is often useful to express the specific detectivity in terms of relative noise levels present in the device. A common expression is given below.

$D^* = \frac{q\lambda \eta}{hc} \left[\frac{4kT}{R_0 A}+2q^2 \eta \Phi_b\right]^{-1/2}$

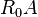With q as the electronic charge, $\lambda$ is the wavelength of interest, h is Planck's constant, c is the speed of light, k is Boltzmann's constant, T is the temperature of the detector, $R_0A$ is the zero-bias dynamic resistance area product (often measured experimentally, but also expressible in noise level assumptions), 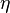$\eta$ is the quantum efficiency of the device, and $\Phi_b$ is the total flux of the source (often a blackbody) in photons/sec/cm².

Detectivity measurement

Detectivity can be measured from a suitable optical setup using known parameters. You will need a known light source with known irradiance at a given standoff distance. The incoming light source will be chopped at a certain frequency, and then each wavelet will be integrated over a given time constant over a given number of frames.

In detail, we compute the bandwidth 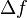$\Delta f$ directly from the integration time constant $t_c$ .

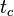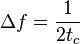
$\Delta f = \frac{1}{2 t_c}$

Next, an rms signal and noise needs to be measured from a set of $N$ frames. This is done either directly by the instrument, or done as post-processing.

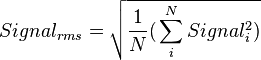
$Signal_{rms} = \sqrt{\frac{1}{N}\big( \sum_i^{N} Signal_i^2 \big)}$

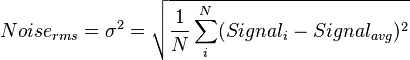
$Noise_{rms} =\sigma^2= \sqrt{\frac{1}{N}\sum_i^N (Signal_i - Signal_{avg})^2}$

Now, the computation of the radiance $H$ in W/sr/cm² must be computed where cm² is the emitting area. Next, emitting area must be converted into a projected area and the solid angle; this product is often called the etendue. This step can be obviated by the use of a calibrated source, where the exact number of photons/s/cm² is known at the detector. If this is unknown, it can be estimated using the black-body radiation equation, detector active area 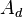$A_d$ and the etendue. This ultimately converts the outgoing radiance of the black body in W/sr/cm² of emitting area into one of W observed on the detector.

The broad-band responsivity, is then just the signal weighted by this wattage.

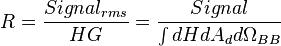
$R = \frac{Signal_{rms}}{H G} = \frac{Signal}{\int dH dA_d d\Omega_{BB}}$

Where,

$R$ is the responsivity in units of Signal / W, (or sometimes V/W or A/W)
$H$ is the outgoing radiance from the black body (or light source) in W/sr/cm² of emitting area
$G$ is the total integrated etendue between the emitting source and detector surface
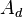$A_d$ is the detector area
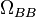$\Omega_{BB}$ is the solid angle of the source projected along the line connecting it to the detector surface.

From this metric noise-equivalent power can be computed by taking the noise level over the responsivity.

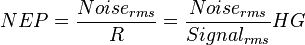
$NEP = \frac{Noise_{rms}}{R} = \frac{Noise_{rms}}{Signal_{rms}}H G$

Similarly, noise-equivalent irradiance can be computed using the responsivity in units of photons/s/W instead of in units of the signal. Now, the detectivity is simply the noise-equivalent power normalized to the bandwidth and detector area.

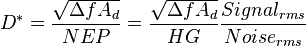
$D^* = \frac{\sqrt{\Delta f A_d}}{NEP} = \frac{\sqrt{\Delta f A_d}}{H G} \frac{Signal_{rms}}{Noise_{rms}}$

References

↑ R. C. Jones, "Quantum efficiency of photoconductors," Proc. IRIS 2, 9 (1957)
↑ R. C. Jones, "Proposal of the detectivity D** for detectors limited by radiation noise," J. Opt. Soc. Am. 50, 1058 (1960), doi:10.1364/JOSA.50.001058)

This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".