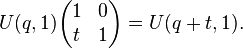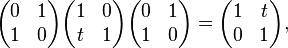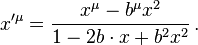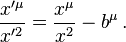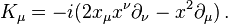Special conformal transformation

In mathematical physics, a special conformal transformation is a type of spherical wave transformation and an expression of conformal symmetry.

Special conformal transformations arise from translation of spacetime and inversion. The inversion can be taken^[1] to be multiplicative inversion of biquaternions B. The complex algebra B can be extended to P(B) through the projective line over a ring. Homographies on P(B) include translations:

U(q,1) \begin{pmatrix}1 & 0 \\ t & 1 \end{pmatrix} = U(q + t, 1).

The homography group G(B) includes

\begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix}1 & 0 \\ t & 1\end{pmatrix}\begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix}1 & t \\ 0 & 1\end{pmatrix},

which provides the action of a special conformal transformation.

Vector presentation

A special conformal transformation can also be written^[2]

x'^\mu = \frac{x^\mu-b^\mu x^2}{1-2b\cdot x+b^2x^2} \,.

It is a composition of an inversion (x^μ → x^μ/x²), a translation (x^μ → x^μ − b^μ), and an inversion:

\frac{x'^\mu}{x'^2} = \frac{x^\mu}{x^2} - b^\mu \,.

K_\mu = -i(2x_\mu x^\nu\partial_\nu - x^2\partial_\mu) \,.

↑ Arthur Conway (1911) "On the application of quaternions to some recent developments of electrical theory", Proceedings of the Royal Irish Academy 29:1–9, particularly page 9
↑ Di Francesco; Mathieu, Sénéchal (1997). Conformal field theory. Graduate texts in contemporary physics. Springer. pp. 97–98. ISBN 978-0-387-94785-3.