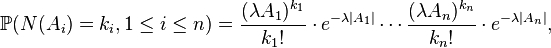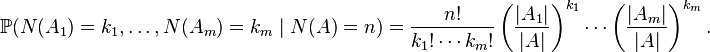Spatial Poisson process
In statistics and probability theory the spatial Poisson process (SPP) is a multidimensional generalization of the Poisson process, which can be described as a counting process where the number of points (events) in disjoint intervals are independent and have a Poisson distribution. Similarly, one can think of "points" being scattered over a  -dimensional space in some random manner and of the spatial Poisson process as counting the number of points in a given set. It is also common to speak of a Poisson point process instead of a SPP.
-dimensional space in some random manner and of the spatial Poisson process as counting the number of points in a given set. It is also common to speak of a Poisson point process instead of a SPP.
Definition
Usually, the SPP is considered on the Euclidean space 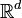 where
where 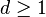 . Firstly it is needed to give some technical definitions.
Likewise to the one-dimensional case a realization of a SPP on
. Firstly it is needed to give some technical definitions.
Likewise to the one-dimensional case a realization of a SPP on 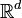 is assumed to be a countable subset
is assumed to be a countable subset 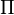 of
of 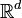 . Thus,
. Thus, 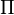 can be seen as a countable set of points. The distribution of
can be seen as a countable set of points. The distribution of 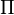 through the number
through the number 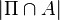 of its points lying in a subset
of its points lying in a subset 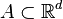 is going to be examined. It is assumed, that there is a well defined notion of the "volume" of
is going to be examined. It is assumed, that there is a well defined notion of the "volume" of  . More Specifically, it is assumed that
. More Specifically, it is assumed that 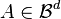 , in other words
, in other words  is in the Borel-
is in the Borel-  algebra. Writing
algebra. Writing 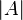 we mean the volume given by the Lebesgue measure of the Borel set
we mean the volume given by the Lebesgue measure of the Borel set  .[1]
.[1]
More generally it is possible to consider a state space 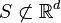 in which the points of a Poisson process sit. Though, it is naturally assumed that
in which the points of a Poisson process sit. Though, it is naturally assumed that  is a measurable space and that its measurable sets form a
is a measurable space and that its measurable sets form a  . It is also possible to define the SPP with a general measure
. It is also possible to define the SPP with a general measure  instead of using the Lebesgue measure. In that case
instead of using the Lebesgue measure. In that case 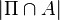 is replaced by
is replaced by 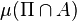 . [2]
. [2]
It is common to distinguish between the homogeneous and inhomogeneous case:
Homogeneous spatial Poisson process
The random countable subset 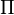 of
of 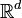 is called a homogeneous spatial Poisson process with (constant) intensity
is called a homogeneous spatial Poisson process with (constant) intensity  if, for all
if, for all 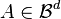 , the random variables
, the random variables 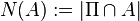 satisfy:[1]
satisfy:[1]
-
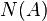 has the Poisson distribution with parameter
has the Poisson distribution with parameter 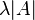 , and
, and - if
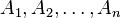 are disjoint sets in
are disjoint sets in 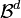 , then
, then 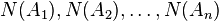 are independent random variables.
are independent random variables.
The counting process  is commonly referred to be itself a Poisson process if it satisfies 1.
and 2. above. The special case when
is commonly referred to be itself a Poisson process if it satisfies 1.
and 2. above. The special case when 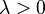 and
and 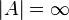 , the situation is interpreted as
, the situation is interpreted as 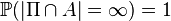 .
.
Inhomogeneous spatial Poisson process
Roughly speaking, the inhomogeneous case differs from the homogeneous case by the intensity  , which is not constant anymore. As indicated above, it is useful to have a definition of a Poisson
process with other measures than Lebesgue measure. In order to get another measure
, which is not constant anymore. As indicated above, it is useful to have a definition of a Poisson
process with other measures than Lebesgue measure. In order to get another measure 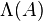 than
than 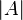 the Euclidean element
the Euclidean element 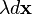 is replaced by the element
is replaced by the element 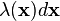 . As a consequence the definition follows
. As a consequence the definition follows
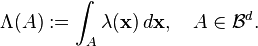
That leads to the following
Definition[1] Let 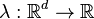 be a non-negative measurable function such that
be a non-negative measurable function such that 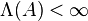 for all bounded
for all bounded  . The random countable subset
. The random countable subset 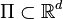 is called inhomogeneous spatial Poisson process with intensity function
is called inhomogeneous spatial Poisson process with intensity function  if, for all
if, for all 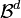 , the random variables
, the random variables 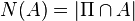 satisfy:
satisfy:
-
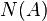 has the Poisson distribution with parameter
has the Poisson distribution with parameter 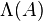 , and
, and - if
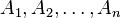 are disjoint sets in
are disjoint sets in 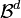 , then
, then 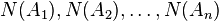 are independent random variables.
are independent random variables.
The function 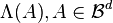 is often called the mean measure of the process
is often called the mean measure of the process 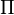 .
.
Examples
Besides the application of the Poisson process in one dimension, there are many examples in two and higher dimensions. Modeling with a spatial Poisson process can be done in the following situations:[1][3]
- The distribution of stars in a galaxy or of galaxies in the universe,
- Positions of animals in their habitat,
- The locations of active sites in a chemical reaction or of the weeds in your lawn,
- Defects on a surface or in a volume in reliability engineering.
- Positionally resolved photo-electron events on a photo-cathode focal plane array.
Even when a Poisson process is not a perfect description of such a system, it can provide a relatively simple yardstick against which to measure the improvements which may be offered by more sophisticated but often less tractable models.
Mathematical properties
Many properties known from the Poisson Process hold also true in the multidimensional process. The Poisson point process is also characterized by the single parameter  . It is a simple, stationary point process with mean measure
. It is a simple, stationary point process with mean measure  . [2]
. [2]
Equivalent formulation
It can be shown, that because of the two essential conditions the distribution of the spatial Poisson process is given by[2]
for any disjoint bounded subsets 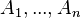 and non-negative integers
and non-negative integers 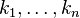 .
.
Derivation from physically postulates
Using the law of rare events the Poisson process can be concluded by certain physically plausible postulates.[3] Let 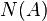 be a random point process fulfilling these postulates, then
be a random point process fulfilling these postulates, then 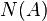 is a homogeneous Poisson Point Process with intensity
is a homogeneous Poisson Point Process with intensity  derived from the postulates and the distribution is given as above in the Equivalent Formulation. Namely the four postulates are:
derived from the postulates and the distribution is given as above in the Equivalent Formulation. Namely the four postulates are:
- The possible values for
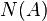 are the nonnegative integers
are the nonnegative integers 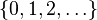 and
and 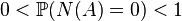 if
if 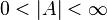 .
. - The probability distribution of
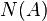 depends on the set
depends on the set  only through its size (length, area, or volume)
only through its size (length, area, or volume) 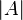 , with the further property that
, with the further property that 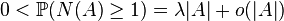 as
as 
- For
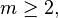 if
if 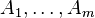 are disjoint regions, then
are disjoint regions, then 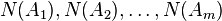 are independent random variables and
are independent random variables and 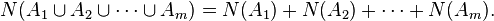
-
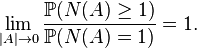
While postulate 1 excludes extreme or trivial cases, the second one asserts that the probability distribution of 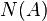 does depend only on the size of
does depend only on the size of  , not on the shape or location. Thirdly it is postulated, that disjoint regions are independent regarding the outcome of the process. Finally, postulate 4 requires that there cannot be tow points occupying the same location.
, not on the shape or location. Thirdly it is postulated, that disjoint regions are independent regarding the outcome of the process. Finally, postulate 4 requires that there cannot be tow points occupying the same location.
Distribution of n points in a given set
We are interested in the distribution of a point from which is supposed to be contained in a region  with positive size
with positive size 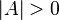 . In other words:
. In other words: 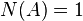 . The question where the point can be found in
. The question where the point can be found in  is answered by a uniform distribution:[3]
is answered by a uniform distribution:[3]
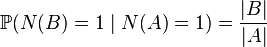 for any set
for any set 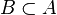
Consider again a region with positive size 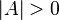 , and suppose now it is known that
, and suppose now it is known that  contains exactly
contains exactly  points. Then, these points are independent and uniformly distributed in
points. Then, these points are independent and uniformly distributed in  in the sense that for any disjoint partition
in the sense that for any disjoint partition 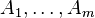 of
of  , and any positive integers
, and any positive integers 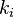 , where
, where 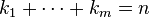 , we have
, we have
Thus, the conditional distribution follows a multinomial distribution.[3]
Other properties
The union of two independent SPP is again a spatial Poisson process:
Superposition Theorem[1] Let 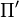 and
and 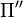 be independent Poisson processes on
be independent Poisson processes on 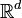 with respective intensity functions
with respective intensity functions 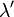 and
and 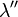 . The set
. The set 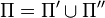 is a Poisson process with intensity function
is a Poisson process with intensity function 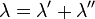 .
.
The theorem can be generalized to the union of more than two processes.
There exist a complementary version to the superposition theorem:
Colouring theorem[1] Let 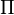 be a non-homogeneous Poisson process on
be a non-homogeneous Poisson process on 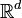 with intensity function
with intensity function 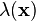 . We colour the points of
. We colour the points of 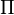 in the following way. A point of
in the following way. A point of 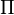 at position x is coloured green with probability
at position x is coloured green with probability 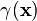 ; otherwise it is coloured scarlet (with probability
; otherwise it is coloured scarlet (with probability 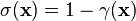 ). Points are coloured independently of one another. Let
). Points are coloured independently of one another. Let
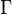 and
and 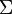 be the sets of points coloured green and scarlet, respectively. Then
be the sets of points coloured green and scarlet, respectively. Then 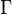 and
and 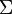 are independent Poisson processes with respective intensity functions
are independent Poisson processes with respective intensity functions 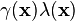 and
and 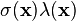 .
.
Generalization
The Spatial Poisson Process is a very common example of a Point process.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 G. R. Grimmett, D. Stirzaker, Probability and Random Processes , Oxford University Press, Third Edition 2001, pages 281–292
- ↑ 2.0 2.1 2.2 J. F. C. Kingman, Poisson Processes, Oxford Studies in Probability, Oxford University Press New York, 1993, pages 11–25
- ↑ 3.0 3.1 3.2 3.3 Mark A. Pinsky, Samuel Karlin, An Introduction to Stochastic Modeling , Elsevier, Fourth Edition 2011, pages 259–263